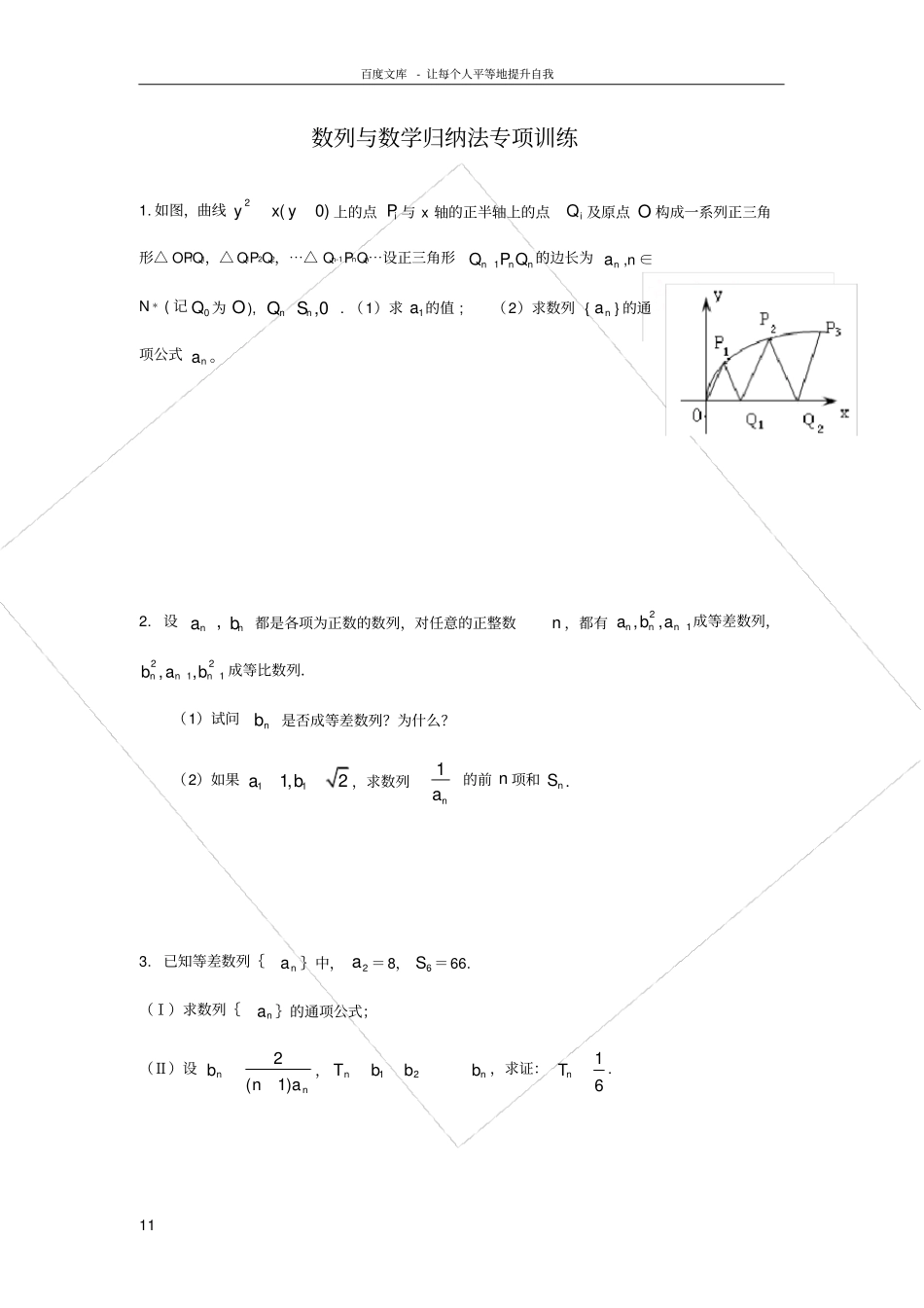
百度文库- 让每个人平等地提升自我11 数列与数学归纳法专项训练1. 如图,曲线2(0)yx y上的点iP 与 x 轴的正半轴上的点iQ 及原点 O 构成一系列正三角形△ OP1Q1,△ Q1P2Q2,⋯△ Qn-1PnQn⋯设正三角形1nnnQP Q 的边长为na ,n ∈N﹡( 记0Q 为 O),,0nnQS. (1)求1a 的值 ; (2)求数列 {na } 的通项公式na 。2. 设,nnab都是各项为正数的数列,对任意的正整数n ,都有21,,nnnaba成等差数列,2211,,nnnbab成等比数列.(1)试问nb是否成等差数列?为什么?(2)如果111,2ab,求数列1na的前 n 项和nS .3. 已知等差数列{na }中,2a =8,6S =66. (Ⅰ)求数列{na }的通项公式;(Ⅱ)设nnanb)1(2,nnbbbT21,求证:nT16. 百度文库- 让每个人平等地提升自我22 4. 已知数列 {na } 中531a,112nnaa(n≥ 2,Nn),数列}{nb,满足11nnab(Nn)(1)求证数列 {nb } 是等差数列;(2)求数列 {na } 中的最大项与最小项,并说明理由;(3)记21bbSn⋯nb ,求1)1(limnnSbnn.5. 已知数列 { an} 中, a1>0, 且 an+1=23na, (Ⅰ) 试求 a1 的值,使得数列{ an} 是一个常数数列; (Ⅱ) 试求 a1 的取值范围 , 使得 an+1>an 对任何自然数n 都成立; (Ⅲ) 若 a1 = 2 ,设 bn = | an+1-an| ( n = 1 ,2,3,⋯ ) ,并以 Sn表示数列 {bn} 的前 n 项的和,求证 : Sn<25 .6. (1)已知:)0(x,求证xxxx11ln11;(2)已知:2nNn且,求证:11211ln13121nnn。7. 已 知 数 列na各 项 均 不 为0 , 其 前n项 和 为nS, 且 对 任 意Nn, 都 有nnpapSp)1((p为大于1的常数),并记nnnnnnnSaCaCaCnf21)(2211. 百度文库- 让每个人平等地提升自我33 (1)求na ;(2)比较)1(nf与)(21nfpp的大小Nn;(3)求证:1212111111)()()12(nnippppifnfn(Nn). 8. 已知 nN ,各项为正的等差数列na满足263521,10aaaa,又数列lgnb的前 n 项和是11 lg312nSn nn n。(1)求数列na的通项公式;(2)求证数列nb是等比数列;(3)设nnnca b ,试问数列nc有没有最大项?如果有,求出这个最大项,如果没有,说明理由。9. 设数列na前项和为ns , 且(3),(32)Nnmmasmnn, 其中 m为常数 ,m.3(1) 求证 : 是等比数列 ; 若 数 列na的 公 比q=f(m),数 列nb满 足),2,)((231,11nNnbfbabnn求证:nb1为等差数列 , 求nb . 百度文库- 让每个人平...