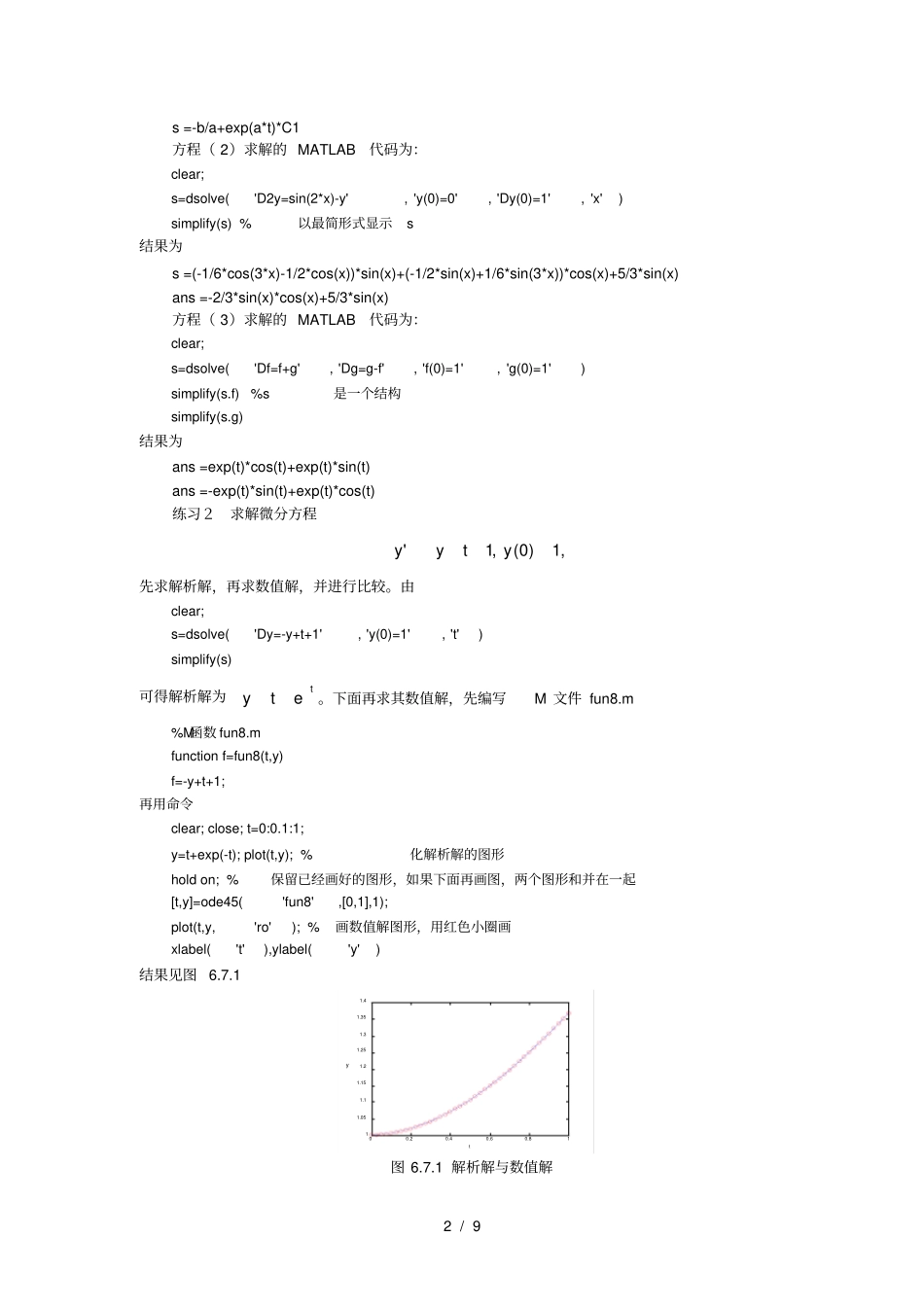
1 / 9 实验六常微分方程的 Matlab 解法一、实验目的1. 了解常微分方程的解析解。2. 了解常微分方程的数值解。3. 学习掌握 MATLAB软件有关的命令。二、实验内容一根长 l 的无弹性细线, 一段固定, 另一端悬挂一个质量为m 的小球,在重力的作用下小球处于垂直的平衡位置。若使小球偏离平衡位置一个角度,让它自由, 它就会沿圆弧摆动。在不考虑空气阻力的情况下,小球会做一定周期的简谐运动。利用牛顿第二定律得到如下的微分方程0)0(',)0(,sin"0mgml问该微分方程是线性的还是非线性的?是否存在解析解?如果不存在解析解,能否求出其近似解?三、实验准备MATLAB中主要用 dsolve 求符号解析解,ode45,ode23,ode15s 求数值解。s=dsolve(‘方程 1’, ‘方程 2’,⋯,’初始条件 1’,’初始条件 2’⋯,’自变量 ’) 用字符串方程表示,自变量缺省值为t。导数用D 表示, 2 阶导数用D2 表示,以此类推。 S 返回解析解。在方程组情形,s 为一个符号结构。[tout,yout]=ode45( ‘yprime ’,[t0,tf],y0) 采 用 变 步 长 四 阶Runge-Kutta法 和 五 阶Runge-Kutta-Felhberg 法求数值解, yprime 是用以表示f(t,y) 的 M 文件名, t0 表示自变量的初始值,tf 表示自变量的终值,y0 表示初始向量值。输出向量tout 表示节点(t 0,t1, ⋯,tn)T,输出矩阵 yout 表示数值解,每一列对应y 的一个分量。若无输出参数,则自动作出图形。ode45 是最常用的求解微分方程数值解的命令,对于刚性方程组不宜采用。ode23 与ode45 类似, 只是精度低一些。 ode12s 用来求解刚性方程组,是用格式同ode45。可以用 help dsolve, help ode45 查阅有关这些命令的详细信息. 四、实验方法与步骤练习 1求下列微分方程的解析解(1)bayy'(2)1)0(',0)0(,)2sin(''yyyxy(3)1)0(',1)0(',','gffgggff方程( 1)求解的 MATLAB代码为:clear; s=dsolve('Dy=a*y+b') 结果为2 / 9 s =-b/a+exp(a*t)*C1 方程( 2)求解的 MATLAB代码为:clear; s=dsolve('D2y=sin(2*x)-y', 'y(0)=0', 'Dy(0)=1', 'x') simplify(s) %以最简形式显示s 结果为s =(-1/6*cos(3*x)-1/2*cos(x))*sin(x)+(-1/2*sin(x)+1/6*sin(3*x))*cos(x)+5/3*sin(x) ans =-2/3*sin(x)*cos(x)+5/3*sin(x) 方程( 3)求解的 MATLAB代码为:clear; s=dsolve('Df=f+g', 'Dg=g-f', 'f(0)=1', 'g(0)=1') simplify(s.f) %s是一个结...