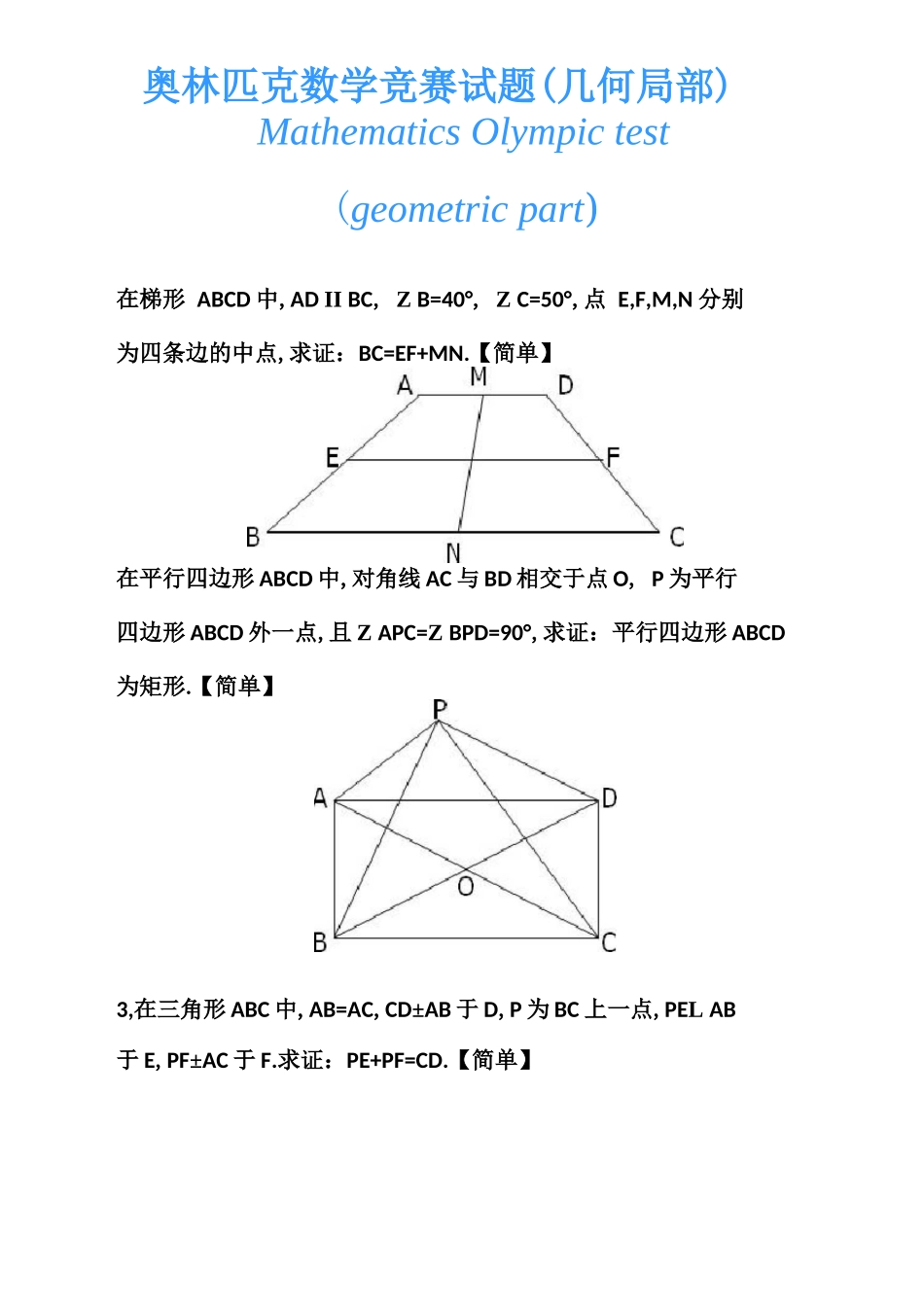
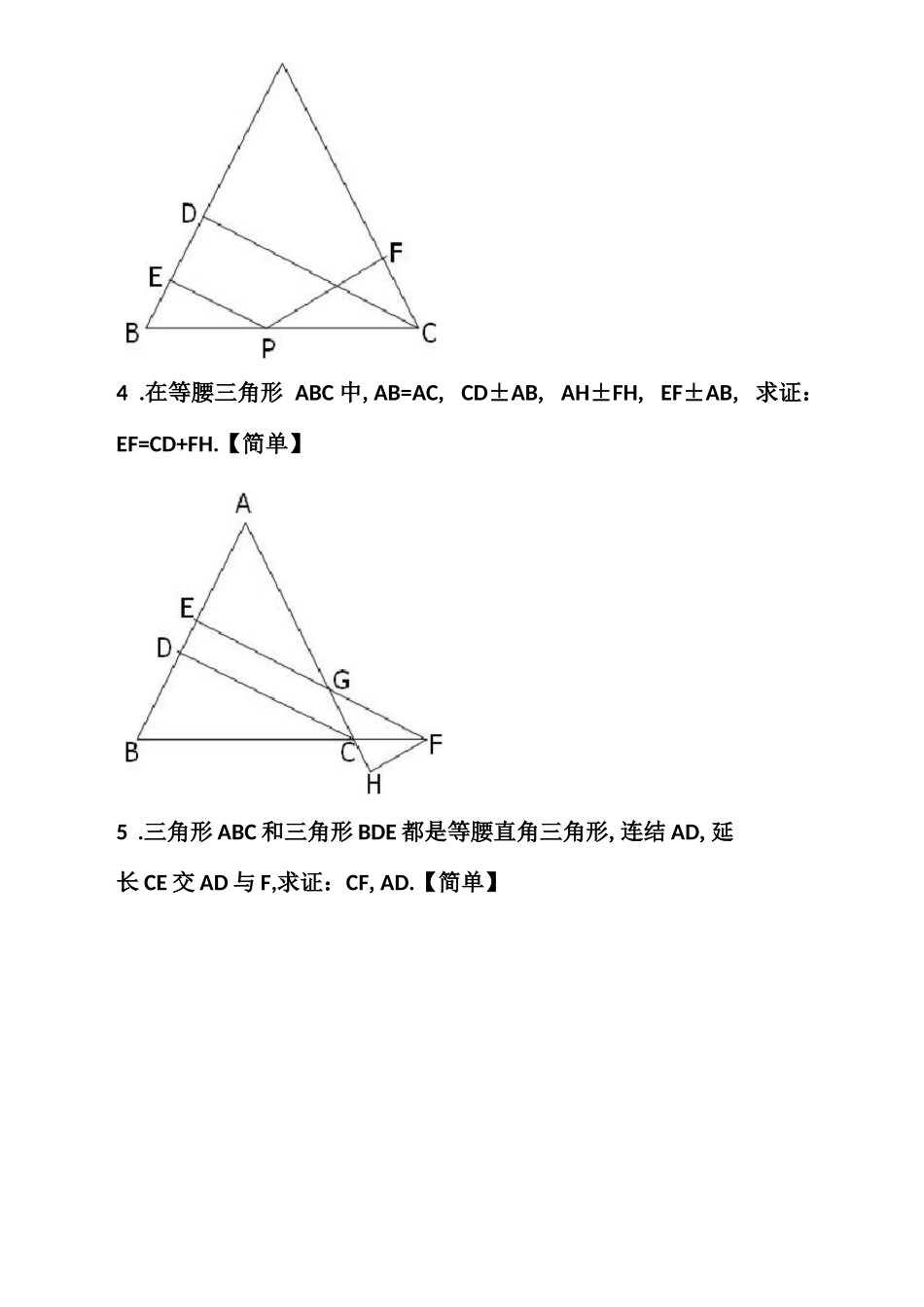
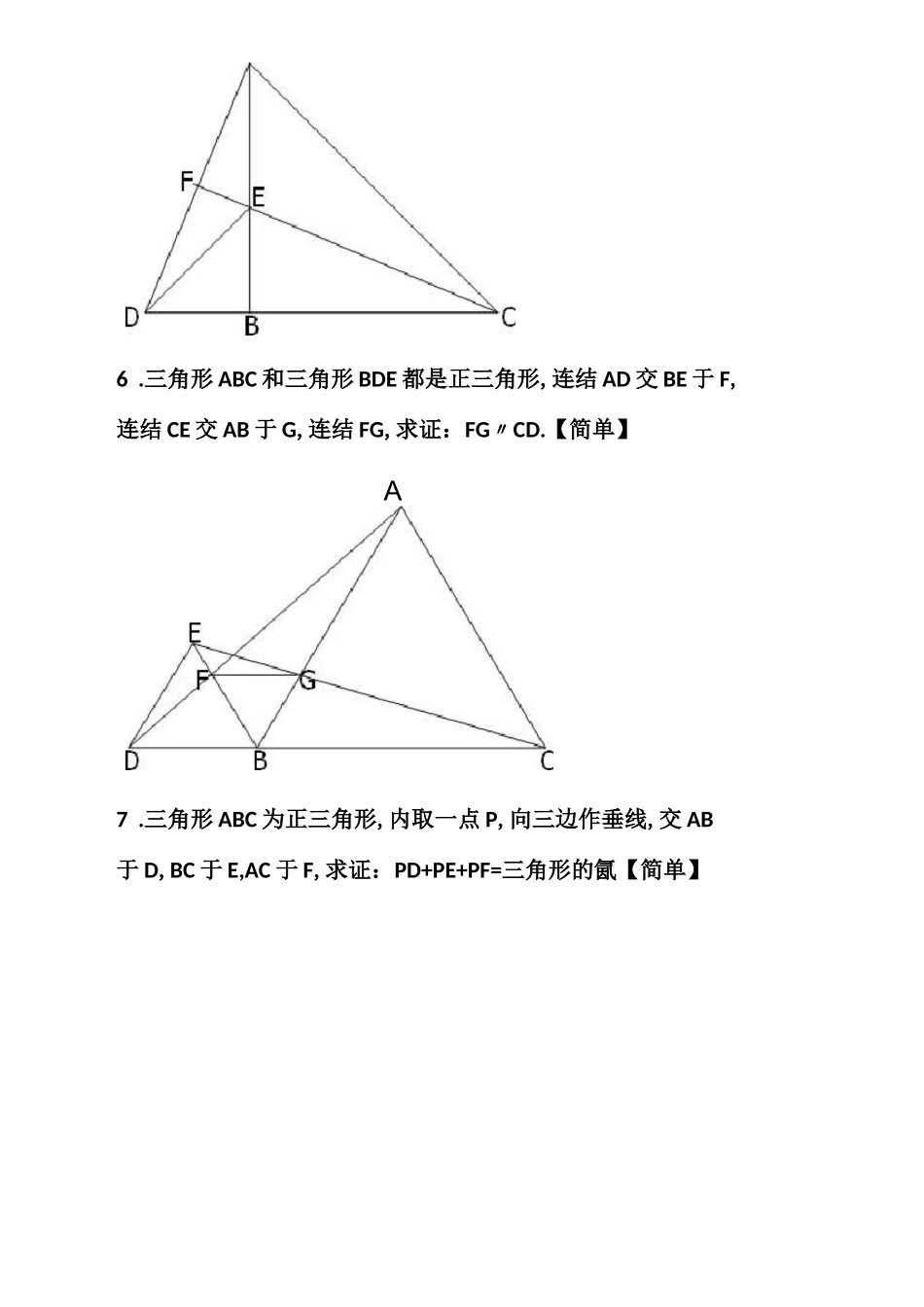
奥林匹克数学竞赛试题(几何局部)Mathematics Olympic test(geometric part)在梯形 ABCD 中,AD II BC, Z B=40°, Z C=50°,点 E,F,M,N 分别为四条边的中点,求证:BC=EF+MN.【简单】在平行四边形 ABCD 中,对角线 AC 与 BD 相交于点 O, P 为平行四边形 ABCD 外一点,且 Z APC=Z BPD=90°,求证:平行四边形 ABCD为矩形.【简单】3,在三角形 ABC 中,AB=AC,CD±AB 于 D,P 为 BC 上一点,PEL AB于 E,PF±AC 于 F.求证:PE+PF=CD.【简单】4 .在等腰三角形 ABC 中,AB=AC, CD±AB, AH±FH, EF±AB, 求证:EF=CD+FH.【简单】5 .三角形 ABC 和三角形 BDE 都是等腰直角三角形,连结 AD,延长 CE 交 AD 与 F,求证:CF,AD.【简单】6 .三角形 ABC 和三角形 BDE 都是正三角形,连结 AD 交 BE 于 F,连结 CE 交 AB 于 G,连结 FG,求证:FG〃CD.【简单】A7 .三角形 ABC 为正三角形,内取一点 P,向三边作垂线,交 AB于 D,BC 于 E,AC 于 F,求证:PD+PE+PF=三角形的氤【简单】B EC8 .三角形 ABC 为正三角形,AD 为高,取三角形外一点 P,向三 边〔或边的延长线〕作垂线,交 AB 的延长线 AE 于 M,交 AC 的延 长线 AF 于N,交 BC 于 Q,求证:PM+PNPQ=AD.【中等】A9 .在矩形 ABCD 中,对角线 AC,BD 相交于 O,DE 平分/ ADC 交AC 于 F,假设/ BDE=15°,求 N COE 的度数.【中等】10 .三角形 ABC 是直角三角形,Z BAC=90°, AD±BC, AE 平分Z CAD, BF 平分 Z ABC,交 AD 于 G,交 AE 于 H,连结 EG,求证:EG II AC.【中等】11 .三角形 ABC 和三角形 BDE 都是正三角形,连结 AE,CD,^ AE 的中点N,取 CD 的中点 M,连结 BM,BN,MN,求证:三角形 BMN 是 等边三角形.【中等】12 .在正方形 ABCD 中,作对角线 AC 的平行线 EG,作 BC=CH,连结 BE,延长 HG 交 BE 于 F,连结 CF,求证:BC=CF.【中等】13 .在直角梯形 ABCD 中,AD//BC,AD=3,BC=5,将腰 CD 绕点D 逆时针旋转 90.至 DE,连结人£,求三角形 ADE 的面积.【中等】14 .在任意四边形 ABCD 中,AB=CD, P,Q,R 分别为 AD,BC,BD 的中点,Z ABD=25°, Z BDC=65°,求 N PQR 的度数.【中等】S 一15 .在梯形 ABCD 中,ADII BC, E 为 AB 的中点,求证: 三角一S 一一S 一形 CDE=三角形 ADE+三角形 BCE・【较难】16 .矩形 ABCD,在 CD 的延长线上取一点 E...