delta机器人反解算法VIP免费

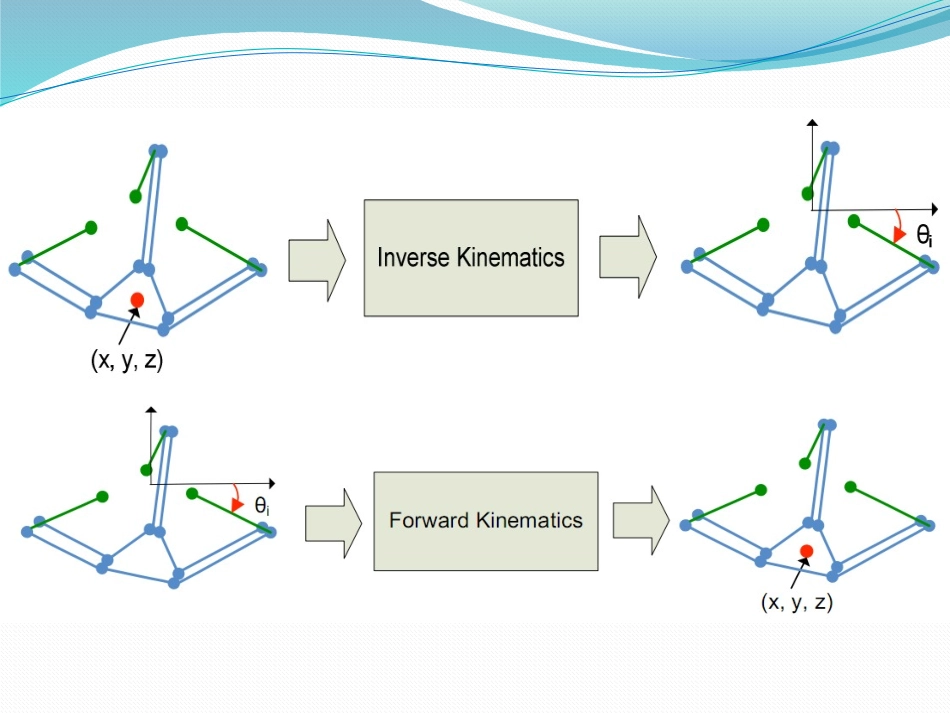
KinematicsAnalysisofaDeltaParalellRobotDelta机器人的反解算法详解InverseKinematics𝑙22−𝑥02=𝑙2′2(EQ-1)𝑑12+𝑑22=𝑙2′2(EQ-2)𝑑12+𝑑22=𝑙22−𝑥02𝑑1=¿𝑑2=𝑧0+𝑙1sin𝜃1(EQ-3)(EQ-4)(EQ-5)Substituting(4),(5)in(3),andsimplifyingWith(EQ-6)Substituting(6)intrigonometricidentities,Where,2𝑇𝑙11−𝑡21+𝑡2+2𝑧0𝑙12𝑡1+𝑡2=𝐾(EQ-7)(K+2T𝑙1)𝑡2+(−4𝑧0𝑙1)𝑡+(𝐾−2𝑇𝑙1)=0(EQ-8)SettingWeobtain(EQ-9)𝑡=−𝑒2±√𝑒22−4𝑒1𝑒32𝑒1)𝜃1=2tan−1（𝑡）=2tan−1(−𝑒2±√𝑒22−4𝑒1𝑒32𝑒1)i=2，∅2=120°i=3，∅3=240°¿[𝑥2𝑦2𝑧2][𝑥3𝑦3𝑧3]i=1，∅1=0°[𝑥1𝑦1𝑧1]𝑒1=K+2T𝑙1𝑒2=−4𝑧𝑖𝑙1𝑒3=K−2T𝑙1T=OA+𝑦𝑖−𝐺′𝐷′=𝑅−𝑦𝑖−𝑟K=𝑙22−𝑥𝑖2−𝑇2−𝑙12−𝑧𝑖2𝜃1𝜃2𝜃3𝜃𝑖=2tan−1（𝑡）=2tan−1(−𝑒2±√𝑒22−4𝑒1𝑒32𝑒1)(EQ-10)MultiplyPciwiththerotationalmatrix𝑅𝑧𝑖𝑅omittedForwardKinematics𝑂𝐹1=𝑂𝐹2=𝑂𝐹3=𝑓2√3𝐽1𝐽1′=𝐽2𝐽2′=𝐽3𝐽3′=𝑒2√3𝐹1𝐽1=𝑟𝑓cos𝜃1𝐹2𝐽2=𝑟𝑓cos𝜃2𝐹3𝐽3=𝑟𝑓cos𝜃3𝐽1′(0,−𝑓2√3−𝑟𝑓cos𝜃1+𝑒2√3,−𝑟𝑓sin𝜃1)𝐽2′([𝑓2√3+𝑟𝑓cos𝜃2−𝑒2√3]×cos𝜋6,[𝑓2√3+𝑟𝑓cos𝜃2−𝑒2√3]×sin𝜋6,−𝑟𝑓sin𝜃2)𝐽3′(−[𝑓2√3+𝑟𝑓cos𝜃3−𝑒2√3]×cos𝜋6,[𝑓2√3+𝑟𝑓cos𝜃3−𝑒2√3]×sin𝜋6,−𝑟𝑓sin𝜃3)𝐽1′(𝑥1,𝑦1,𝑧1),𝐽2′(𝑥2,𝑦2,𝑧2),𝐽3′(𝑥3,𝑦3,𝑧3)Threeballequationsas:(𝑥−𝑥1)2+(𝑦−𝑦1)2+(𝑧−𝑧1)2=𝑟𝑒2(𝑥−𝑥2)2+(𝑦−𝑦2)2+(𝑧−𝑧2)2=𝑟𝑒2(𝑥−𝑥3)2+(𝑦−𝑦3)2+(𝑧−𝑧3)2=𝑟𝑒2Twosolutions:z>0z<0x(z)y(z)√√xTest&VerifyinMatlab23580020045DeltaRobotForward(-18,13,30,235,800,200,45)z=-703.0740x=80.7752y=-200.2409DeltaRobotInverse(80.7752,-200.2409,-703.0740,235,800,200,45)theta11=-18.0000theta21=13.0000theta31=30.0000theta12=-169.3635theta22=-163.4904theta32=-160.3721RobotickinematicsCross-Product𝑛×𝑜=¿xyzxyzxyzijknnnaiajakooo()()()yzzyxzzxxyyxxyzinonojnonoknonoaiajakDot-Product0no0na0ao1n1o1a向量的长度必须为10xxyyzznonono0xxyyzznanana0xxyyzzaoaoao2221xyznnn2221xyzooo2221xyzaaa0001xxxxyyyyobjectzzzznoapnoapFnoap12条信息：9条姿态信息，3条位置信息6个自由度：3个平动，3个转动相对于运动坐标系（也就是当前坐标系）的n轴而不是参考坐标系的x轴旋转90度。为计算当前坐标系中的点的坐标相对于参考坐标系的变化，这时需要右乘变换矩阵而不是左乘。由于运动坐标系中的点或物体的位置总是相对于运动坐标系测量的，所以总是右乘描述该点或物体的位置矩阵。0001xxxxyyyyzzzznoapnoapFnoap10001xyzxyzxyznnnPnoooPoFaaaPa0.500.86630.86605201050001T10.50.8660(30.520.86650)001(302051)0.8660.50(30.86620.550)0001TExample谢谢！未完待续，敬请期待