材料力学复杂应力状态的最大应力VIP免费

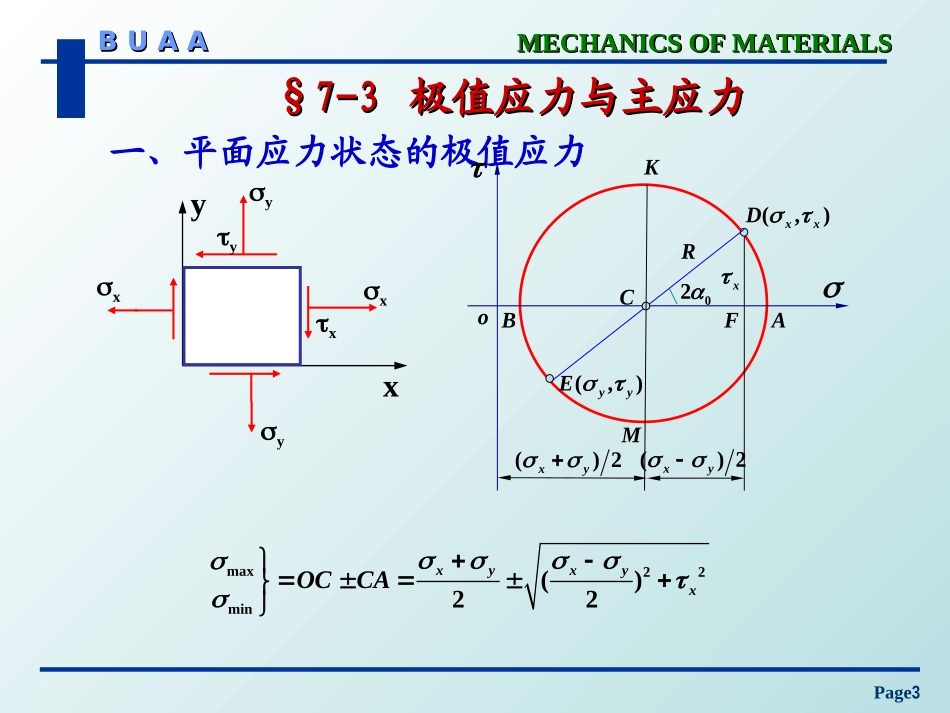
MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage1作业：7-6(c),7-7,7-9,7-13MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage2本讲内容本讲内容§7-5§7-5广义胡克定律广义胡克定律§7-4§7-4复杂应力状态的最大应力复杂应力状态的最大应力§7-3极值应力与主应力MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage3xyxxxyyymax22min()22xyxyxOCCA一、平面应力状态的极值应力ABRxKM(,)xxD()2xy()2xy(,)yyE02FoC§7-3§7-3极值应力与主应力极值应力与主应力MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage4xyxxxyyy22minmax)2(2xyxyx最大正应力所在截面的方位角0可确定：yxxCFDFtg22020负号表示由x面顺时针方向转至max作用面0o(x+y)/2CDEyx(x-y)/2xyBAFD’yxxxBFDFtgmaxmin0max所在截面的方位角0也可表示为：maxmax0MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage5200o(x+y)/2CDEyx(x-y)/2xyBAFD’maxKM22minmax)2(xyx切应力极值截面与正应力极值截面成45o夹角以上讨论，仅限于//z轴的各截面，故为极值应力sin(2)cos(2)2xyxMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage6二、主应力主平面－切应力为零的截面主应力－主平面上的正应力主应力符号与规定－321主平面微体－相邻主平面相互垂直，构成一正六面形微体（按代数值排列）123正应力极值所在截面的切应力为零MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage7应力状态的分类：根据主应力的数值，将应力状态分为三类：单向应力状态:仅有一个不为零的主应力；二向应力状态:有两个不为零的主应力；三向应力状态:有三个不为零的主应力；复杂应力状态单向应力状态纯剪切状态MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage8Cmaxt,Dmaxc,minmax0231,三、纯剪切状态的最大应力o0,A0,BCD4545,maxC,maxtMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage9（塑性材料）圆轴扭转时滑移与剪断发生在max的作用面：（脆性材料）圆轴扭转时断裂发生在max的作用面：例：纯剪应力状态下不同的断裂机理：MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage10222max2min80MPa1050105030340MPa2222xyxyx解：1.解析法10MPax50MPay303MPa=51.96MPax例：试用解析法与图解法确定主应力的大小和方向1030350单位：MPaMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage111.解析法(续)min40MPa＝max80MPa＝02tan23xxy0602120问题：哪一个解是正确的？060根据对应切应力所指方向可判断的方向1103035013又解：试比较两个求的公式00minmaxtan3xxxy060MECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAMECHANICSOFMATERIALSMECHANICSOFMATERIALSBUAABUAAPage12（2）量A、B两点坐标，BD’的方位角得1=80MPa3=40MPa－060...