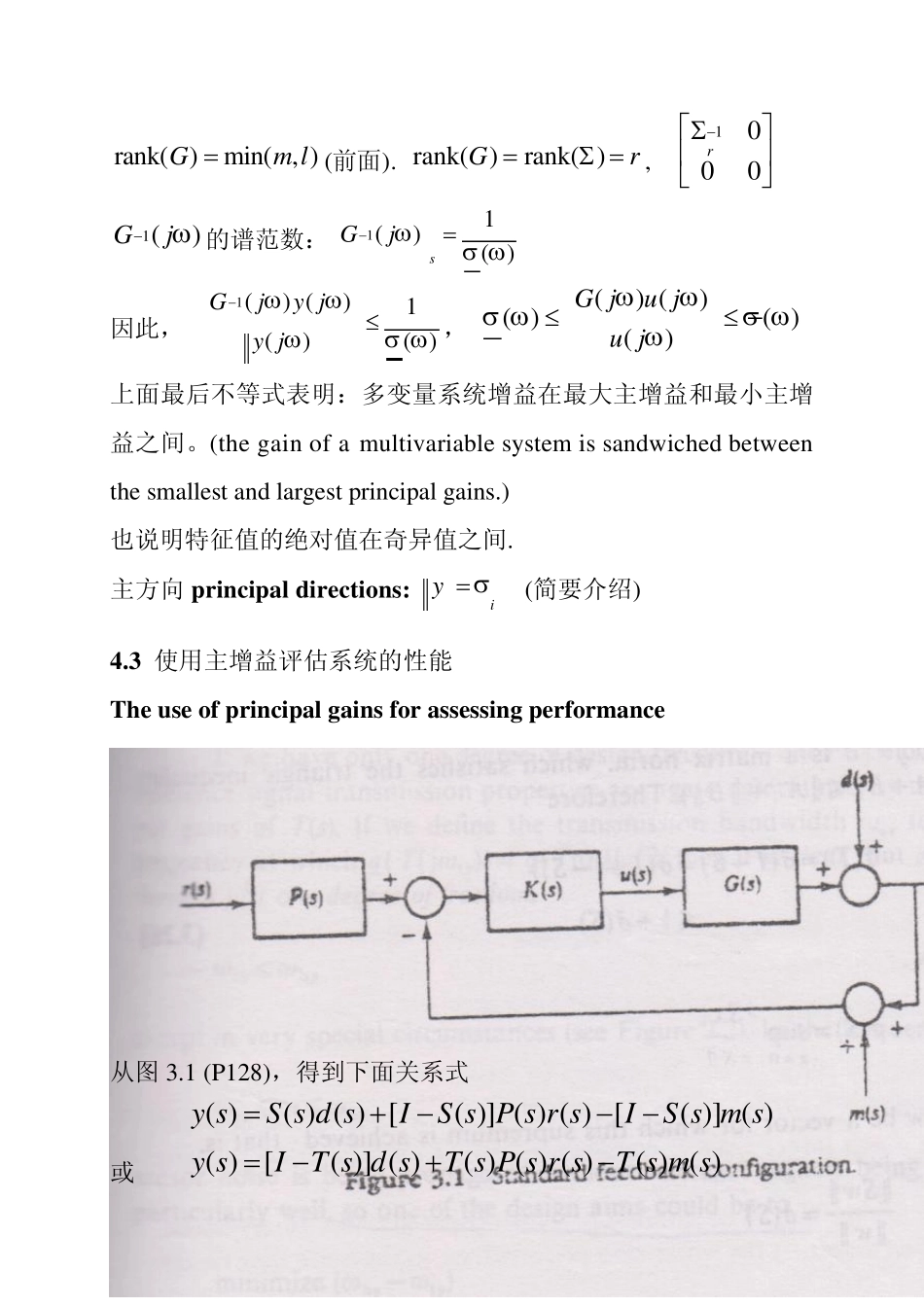
第四章 多变量反馈系统的性能和鲁棒性 Performance and Robustness of Multivariable Feedback Systems 本章内容: 主增益principal gains (奇异值singular values) 系统性能的评估assessing performance 特征轨迹characteristic loci 算子范数operator norms 利用算子范数说明性能 不确定的表示representations of uncertainty 稳定性鲁棒stability robustness 性能鲁棒performance robustness 4.1 Introduction 使用反馈的目的:减少不确定性的影响; 镇定不稳定系统。 不确定性:环境的扰动和噪声(disturbance and noise); 系统本身的行为变化的不可预知(unpredictable ways)。 系统的性能:输出跟踪参考输入的能力 系统的鲁棒性:在外部扰动下系统回复原状的能力 4.2 主增益Principal gains (singular values) 在 SISO 系统中:稳定裕度(stability margins)和暂态响应(transient response)可以由开环频率特性确定(增益特性gain characteristic)。 MIMO 系统:增益不唯一,即 ( ) ( )G s u s依赖于( )u s 的方向(解释)。因此,研究的思路:从SISO 系统单一的增益到MIMO 系统限制增益的范围,即使用矩阵范数限制比值: 1( ) ( )( ) ( ) , ( )( )Gs y sG s u su sy s 定义从向量的范数到诱导的矩阵范数 Hxx x ――欧氏范数(Euclidean vector norm) 0( )supxGxG sx ――诱导的矩阵范数 sG ――Hilbert 范数或谱范数(spectral norm) G 的奇异值(singular values): HG G或HGG的正特征值的平方根 ( )G s 的主增益(principal gains): ()G j 的奇异值 一般假设:120m 称, 为最大,最小主增益, ( ())()sG jG j 注意( ())G j与频率相关,与2G,G 不同。 奇异值分解(the singular value decomposition---SVD): , , , HHHm lGY UGY YIU UI orthogonal matrix 22, HHHHGGYYG GUU 12diag{,,,}m 1, , HHUYHGHHGHGG, †GH †G 表示G 的伪逆(pseudo-inverse),也直接表示为1G 。 rank( )min( , )Gm l(前面). rank( )rank( )Gr , 1000r 1()Gj的谱范数:11()( )sGj 因此, 1() ()1()( )Gjy jy...