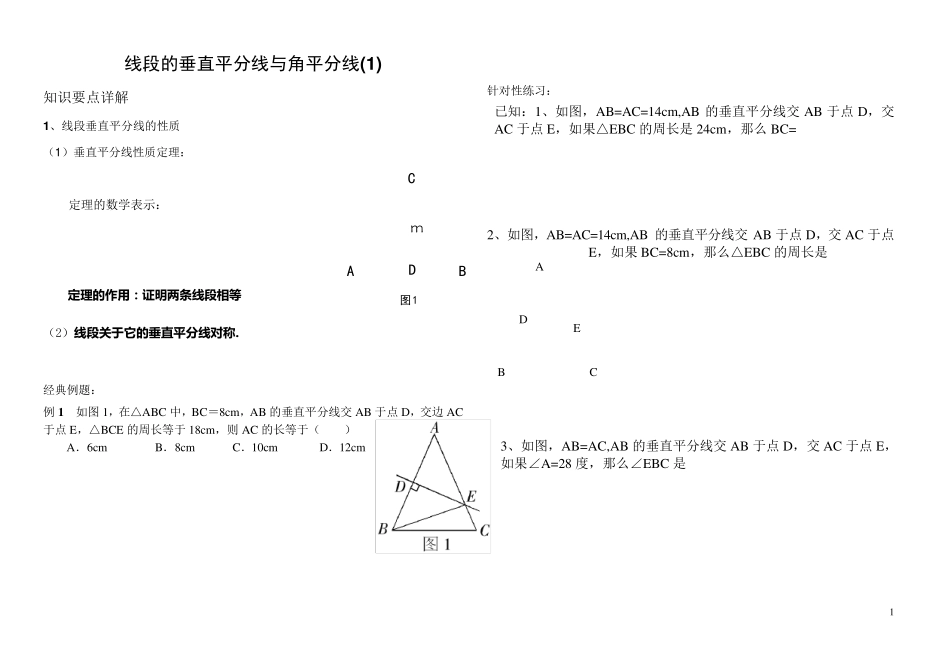
1 线段的垂直平分线与角平分线(1 ) 知识要点详解 1 、线段垂直平分线的性质 (1 )垂直平分线性质定理: 定理的数学表示: 定 理 的 作 用 : 证 明 两条线段相等 (2)线段关于它的 垂直平分线对称. 经典例题: 例1 如图1,在△ABC 中,BC=8cm ,AB 的垂直平分线交AB 于点D,交边AC于点E,△BCE 的周长等于18cm ,则AC 的长等于( ) A.6cm B.8cm C.10cm D.12cm 针对性练习: 已知:1、如图,AB=AC=14cm ,AB 的垂直平分线交AB 于点D,交AC 于点E,如果△EBC 的周长是24cm ,那么BC= 2、如图,AB=AC=14cm ,AB 的垂直平分线交AB 于点D,交AC 于点E,如果BC=8cm ,那么△EBC 的周长是 3、如图,AB=AC,AB 的垂直平分线交AB 于点D,交AC 于点E,如果∠A=28 度,那么∠EBC 是 m图1DABC C E B D A 2 2 、线段垂直平分线性质定理的逆定理 (1)线段垂直平分线的逆定理: 定理的数学表示: 定 理 的 作 用 : 证 明 一个点在某线段的 垂直平分上. 例2 .如图,已知:在ABC中,90C,30A,BD 平分ABC交AC于D.求证:D 在AB 的垂直平分线上. 针对性练习: 已知:在△ABC 中,ON 是AB 的垂直平分线,OA=OC 求证:点O 在BC 的垂直平分线 例3 、如图8,已知AD 是△ABC 的BC 边上的高,且∠C=2∠B, 求证:BD=AC+CD. 证 明 : 例4 .如图,已知:AD 平分BAC,EF垂直平分AD,交BC 延长线于F,连结 AF。求证: CAFB。 m图 2DABC图 8BCDAB A C O N 3 3 、关于三角形三边垂直平分线的定理 (1)关于三角形三边垂直平分线的定理: 定理的数学表示: 定理的作用:证 明 三角形内的线段相等. (2)三角形三边垂直平分线的交点位置与三角形形状的关系: 课堂练习: 1.如图,AC=AD,BC=BD,则( ) A.CD 垂直平分AD B.AB 垂直平分CD C.CD 平分∠ACB D.以上结论均不对 2.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形 3.下列命题中正确的命题有( ) ①线段垂直平分线上任一点到线段两端距离相等; ②线段上任一点到垂直平分线两端距离相等; ③经过线段中点的直线只有一条; ④点P 在线段AB 外且PA=PB,过P 作直线MN,则MN 是线段AB 的垂直平分线; ⑤过线段上任一点可以作这条线段的中垂线. A.1 ...