任意角的三角比VIP免费

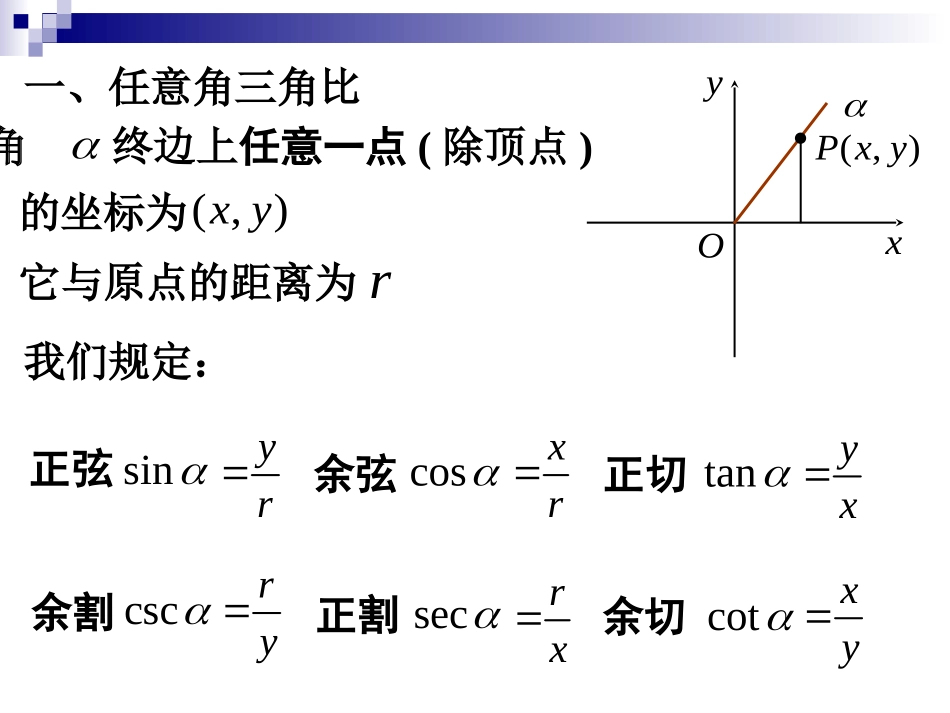
第五章三角比5.2.1任意角的三角比回顾锐角三角比OMPsinMPOPcosOMOPtanMPOMAB角正弦、余弦、正切值是如何定义的？正弦余弦正切1ccinss1scosec1cottan余割正割余切sin角终边上任意一点(除顶点)正弦余弦正切余割正割余切一、任意角三角比(,)xy的坐标为r(,)PxyxyO它与原点的距离为我们规定：yrcosxrtanyxcscrysecrxcotxy例1.已知角的终边经过点，求角的六个(2,1)P三角比值.解：2,1xy因此22(2)15rsinyr1555cosxr25255tanyx1212cscry5secrx52cotxy2220rxy例2.求角的正弦、余弦和正切值.53解：在直角坐标系中作角53AOB60OxyPAM300在终边上取点P且满足：1OP3POM13(,)22P即13,,122xyr5sin35cos332125tan33解毕B例3.求下列各角的六个三角比值.(1)0(2)解:(1)0时sin00cos01tan00csc0sec01cot0不存在不存在(2)时,3sin23cot023csc23sec23tan2不存在不存在13cos2012)0,1(P取23)1,0(P取二、三角比有意义的条件sinyrRcosxrRtanyx,2kkZ设为角终边上一点(,)PxyOPr(0)rcscry,kkZsecrx,2kkZcotxy,kkZ第五章三角比5.2.2任意角的三角比三角函数线回顾锐角三角比任意角三角比OMPABsinMPOPcosOMOPtanMPOM正弦余弦正切(,)PxyxyOsin正弦余弦正切yrcosxrtanyxOPxy1sin,cos11yxyx(cos,sin)P一、正弦值、余弦值和正切值的几何表示PxM过作轴的垂线，垂足为设单位圆的圆心在原点，角的终边与单位圆交于点(,)PxyM思考哪个几何量可以表示？sin哪个几何量可以表示？cossin,cosMPOMPxM过作轴的垂线，垂足为设单位圆的圆心在原点，角的终边与单位圆交于点(,)Pxysin,cosMPOM思考是否存在关于的类似结论？tan一、正弦值、余弦值和正切值的几何表示(1,0)A过作单位圆的切线，交角的终边于点TtanMPATOMOAtanATOPxy1MATPxM过作轴的垂线，垂足为设单位圆的圆心在原点，角的终边与单位圆交于点(,)Pxysin,cos,tanMPOMAT思考这些结论是否对于任意角都成立？OPxy1MAT(1,0)A过作单位圆的切线，T交角的终边与点一、正弦值、余弦值和正切值的几何表示OPxy1MATOPxy1MATOPxy1MATxOPy1MAT规定：有向线段一、正弦值、余弦值和正切值的几何表示,,MPOMAT与坐标轴同向时，其数量为正值.与坐标轴反向时，其数量为负值.二、正弦线、余弦线与正切线PxM过作轴的垂线，垂足为设单位圆的圆心在原点，角的终边与单位圆交于点POPxy1MAT(1,0)A过作单位圆的切线，T交角的终边(或其反向延长线)于点有向线段称为的正弦线，即MPsinMP有向线段称为的余弦线，即OMcosOM有向线段称为的正切线，即ATtanAT第五章三角比5.2.2任意角的三角比诱导公式I,II例.试利用计算器确定下列各三角比的符号.cos260(1)4sin3(2)tan(495)(3)4tan7(4)解:(1)cos2600.1740(2)4sin0.86630(3)tan(495)10(4)4tan4.38107思考：各象限角的正弦、余弦和正切的符号？三、象限角的三角比的符号++++++______sincostan思考：各象限角的余切、正割和余割的符号？例.确定下列三角比值的符号313cos).1()4sin().2()556tan().3(0其中第(1)小题三角比的值是什么？一、角与的三角函数值的关系2,kkZ角与终边相同，2,kkZ它们的同名三角比相等.OPxyMT1A(2)ksin(2)kcos(2)ktan(2)ksincostan第I组诱导公式思考cot(2)?kcot一、角与的三角函数值的关系2,kkZ角与终边相同，2,kkZ它们的同名三角比相等.OPxyMT1A(2)ksin(2)kcos(2)ktan(2)ksincostan第I组诱导公式作用：绝对值较大的角的三角比化为绝对值较小的角的三角比例.利用...