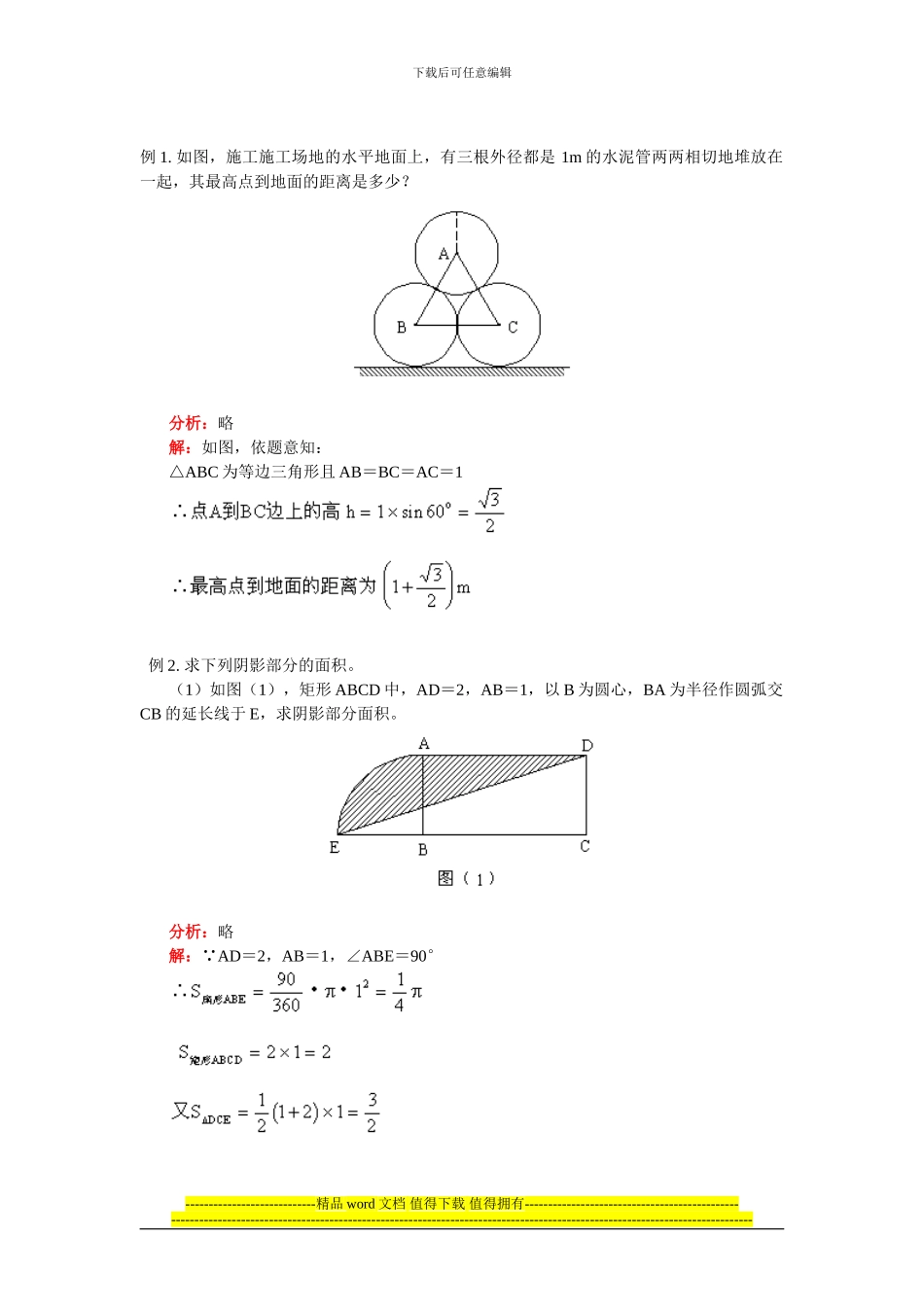
下载后可任意编辑例 1. 如图,施工施工场地的水平地面上,有三根外径都是 1m 的水泥管两两相切地堆放在一起,其最高点到地面的距离是多少? 分析:略 解:如图,依题意知: △ABC 为等边三角形且 AB=BC=AC=1 例 2. 求下列阴影部分的面积。 (1)如图(1),矩形 ABCD 中,AD=2,AB=1,以 B 为圆心,BA 为半径作圆弧交CB 的延长线于 E,求阴影部分面积。 分析:略 解:∵AD=2,AB=1,∠ABE=90° ----------------------------精品 word 文档 值得下载 值得拥有---------------------------------------------------------------------------------------------------------------------------------------------------------------------------下载后可任意编辑 (2)如图(2),AB 是半圆的直径,AB=2R,C、D 为半圆的三等分点,求阴影部分的面积。图(2) 分析:略 解:连结 OC、OD ∴CD∥AB 例 3. 如图,半径是 10cm 的纸片,剪去一个圆心角是 120°的扇形(图中阴影部分),用剩余部分围成一圆锥,求圆锥的高和底面圆的半径。 分析:----------------------------精品 word 文档 值得下载 值得拥有---------------------------------------------------------------------------------------------------------------------------------------------------------------------------下载后可任意编辑高则利用勾股定理。 解:设底面圆的半径为 r,圆锥的高为 h,母线长为 a,则 a=10cm 答: 例 4. 如图,两根圆柱形钢件,它们的半径分别为 6cm 和 2cm,现有一根绳子把它们捆紧,问至少需要多长绳子。(不计绳子接头) 分析:略 解:连结 AB、AC、BD,过点 B 作 BE⊥AC 于 E ∵CD 切⊙A 于 C,切⊙B 于 D ∴AC⊥CD,BD⊥CD ∴BE=CD,BD=CE ----------------------------精品 word 文档 值得下载 值得拥有---------------------------------------------------------------------------------------------------------------------------------------------------------------------------下载后可任意编辑 例 5. (1)求证:CE∥FD; 分析:略 (1)证明:连结 AB ∵∠D=∠ABE,∠ECA=∠ABE ∴∠D=∠ECA ∴CE∥FD----------------------------精品 word 文档 值得下载 值得拥有---------------------------------------------------------------------------------------------------------------------------------------------------------------------------下载后可任意编辑 (2)证明: (3)解: ∵由(2)知:△ECG∽△EBC 又∵EC∥FD,∴△ECG∽△FDG ----------------------------精品 word 文档 值得下载 值得拥有---------------------------------------------------------------------------------------------------------------------------------------------------------------------------