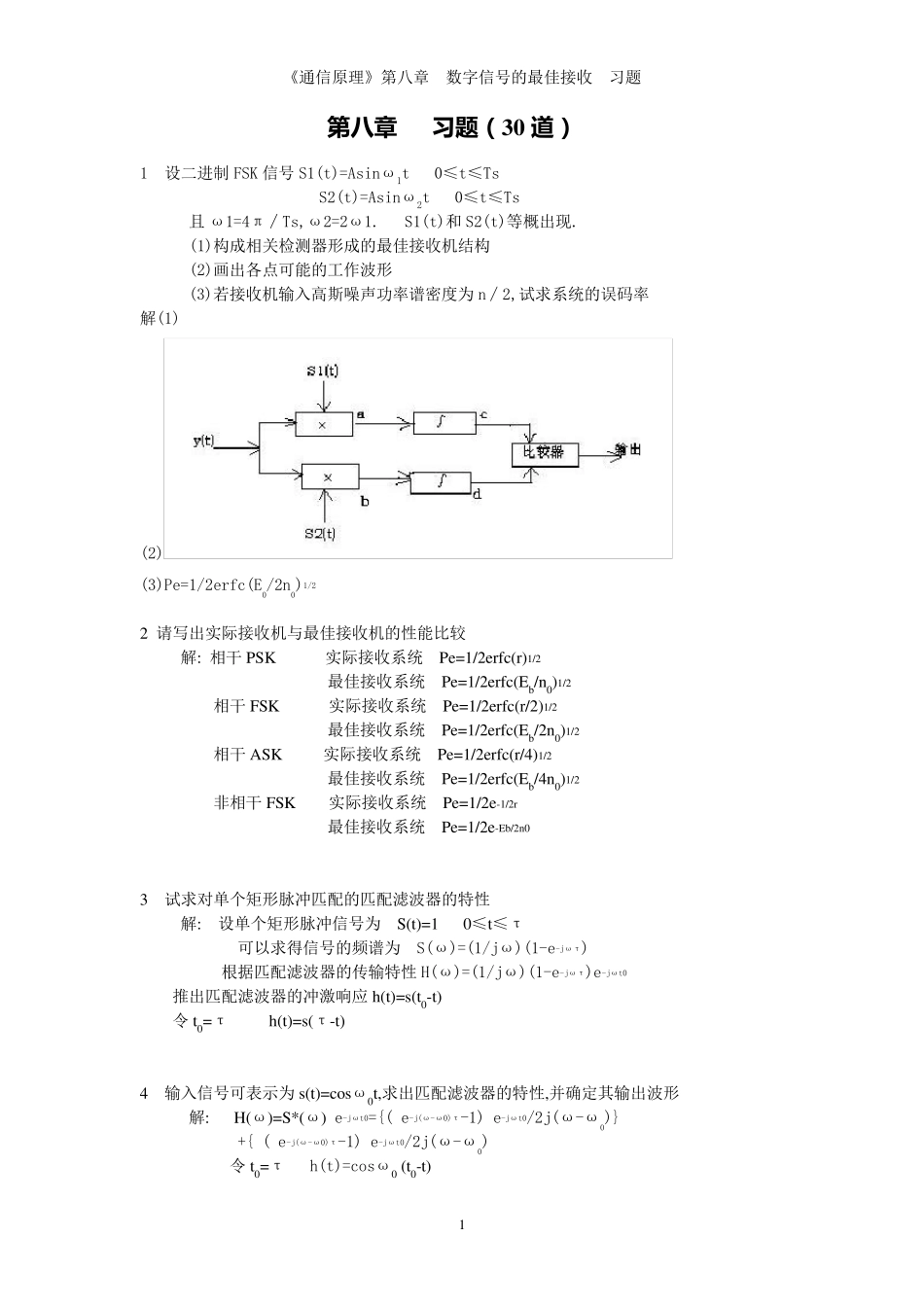
《通信原理》第八章 数字信号的最佳接收 习题 1 第 八 章 习题(3 0 道) 1 设二进制FSK 信号S1(t)=Asinω1t 0≤t≤Ts S2(t)=Asinω2t 0≤t≤Ts 且ω1=4π∕Ts,ω2=2ω1. S1(t)和 S2(t)等概出现. (1)构成相关检测器形成的最佳接收机结构 (2)画出各点可能的工作波形 (3)若接收机输入高斯噪声功率谱密度为 n∕2,试求系统的误码率 解(1) (2) (3)Pe=1/2erfc(E0/2n0)1/2 2 请写出实际接收机与最佳接收机的性能比较 解: 相干 PSK 实际接收系统 Pe=1/2erfc(r)1/2 最佳接收系统 Pe=1/2erfc(Eb/n0)1/2 相干 FSK 实际接收系统 Pe=1/2erfc(r/2)1/2 最佳接收系统 Pe=1/2erfc(Eb/2n0)1/2 相干 ASK 实际接收系统 Pe=1/2erfc(r/4)1/2 最佳接收系统 Pe=1/2erfc(Eb/4n0)1/2 非相干 FSK 实际接收系统 Pe=1/2e-1/2r 最佳接收系统 Pe=1/2e-Eb/2n0 3 试求对单个矩形脉冲匹配的匹配滤波器的特性 解: 设单个矩形脉冲信号为 S(t)=1 0≤t≤τ 可以求得信号的频谱为 S(ω)=(1/jω)(1-e-jωτ) 根据匹配滤波器的传输特性 H(ω)=(1/jω)(1-e-jωτ)e-jωt0 推出匹配滤波器的冲激响应 h(t)=s(t0-t) 令 t0=τ h(t)=s(τ-t) 4 输入信号可表示为 s(t)=cosω0t,求出匹配滤波器的特性,并确定其输出波形 解: H(ω)=S*(ω) e-jωt0={( e-j(ω-ω0)τ-1) e-jωt0/2j(ω-ω0)} +{ ( e-j(ω-ω0)τ-1) e-jωt0/2j(ω-ω0) 令 t0=τ h(t)=cosω0 (t0-t) 《通信原理》第八章 数字信号的最佳接收 习题 2 So(t)=∫S(t)h(t-τ)= (t/2) cosω0t 0≤t≤τ [(2τ-t)/2] cosω0t τ≤t≤2τ 0 其他 t 5 在功率谱密度为 no/2 的高斯白噪声下,设计一个如图所示的的f(t)的匹配滤波器 (1)如何确定最大输出信噪比的时刻? (2)求匹配滤波器的冲击响应和输出波形,并绘出图形. (3)求最大输出信噪比的值 解: (1) 最大输出信噪比出现时刻应在信号结束之后 t0≧T (2) 匹配滤波器的冲击响应为 h(t)=f(t0-t) 输出为 Y(t)=h(t)*f(t) 《通信原理》第八章 数字信号的最佳接收 习题 3 (3)最大信噪比值为 R0MAX=2E/n0=2A2T/N0 6 在S(t)如图(a)所示,h1(t),h2(t),分别如图(b)所示,试画出他们的输出波形,并分别说明他们是否是 s(t)的匹配滤波器 解: y 1(t)=s(t)*h1(t) 其输出波形为 《通信原理》第八章 数字信号的最佳接收 习题 4 y2(t)=s(t)*h2(t) 其输出波形为 显然,在t=T 时刻...