应力圆的概念VIP免费

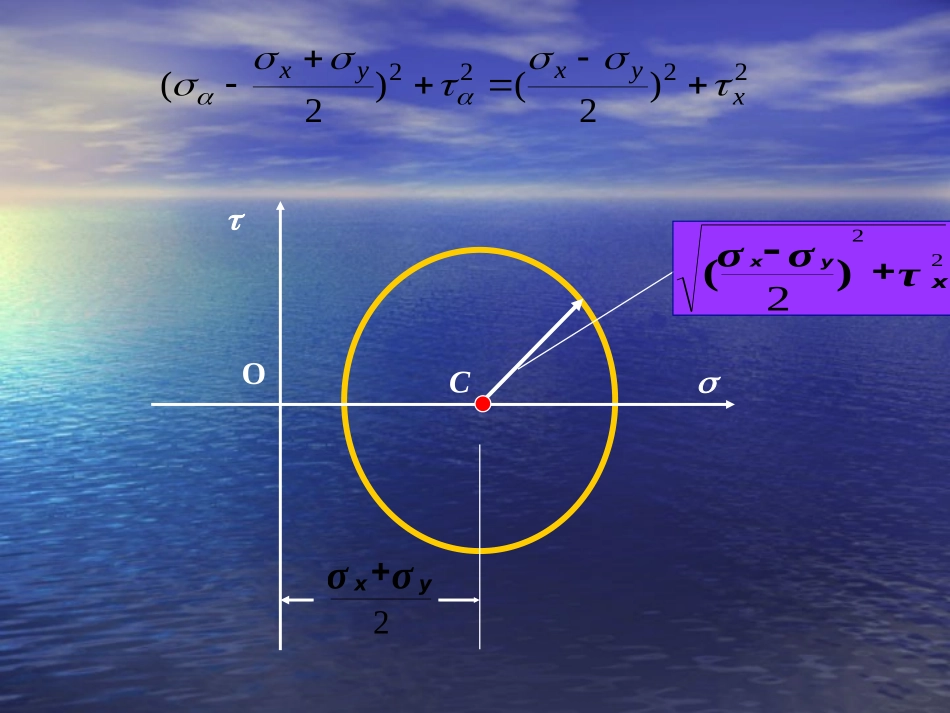
一、应力圆的概念由2cos2sin22sin2cos22xyxxyxyx削去α得到2222)2()2(xyxyx§7-3二向应力状态下的应力分析(应力圆)22)2(xyx当斜截面随方位角变化时,其上的应力,在-直角坐标系内的轨迹是一个圆,圆心位于横坐标轴(轴)上,离原点的距离为半径为此圆习惯上称为应力圆,或称为莫尔圆。2yxσατα2222)2()2(xyxyx2222)2()2(xyxyx2σσyxCOτσσ222xyx)(o二、应力圆作法D1量取OB1=x,B1D1=x,得D1点B1xx在-坐标系内,选定比例尺σxτxσyτyτxσxτyσyσxτxσyτyτxσxτyσyo(b)B1xxD1量取OB2=y,B2D2=y,得D2点D2yB2yσxτxσyτyτxσxτyσyo(b)B1xxD1yyB2D2连接D1D2两点的直线与轴相交于C点,以C为圆心,CD1或CD2为半径作圆Co(b)B1xxyyB2D2C2yx该圆的圆心C点到坐标原点的距离为22)2(xyx半径为该圆就是相应于该单元体应力状态的应力圆D1点的坐标为(x,x)因而D1点代表单元体x平面上的应力。D1σxτxσyτyτxσxτyσyxD2oB1xxyyB2Cef三、利用应力圆求单元体上任一截面上的应力从应力圆的半径CD1按方位角的转向转动2,得到半径CE,圆周上E点的¸坐标就依次为¸。。（证明略）22EEσαταD1说明说明点面之间的对应关系：单元体某一面上的应力，必对应于应力圆上某一点的坐标。夹角关系：圆周上任意两点所引半径的夹角等于单元体上对应两截面夹角的两倍。两者的转向一致。ABoA1B1c2O四、利用应力圆求主应力数值和主平面位置xD1yyB2D2Cσ1A1A2σ2主应力数值B1σxA1和A2两点为与主平面对应的点，其横坐标为主应力1,211CAOCOACAOCOA122σσyxOC221)2(xyxCAoxA1σ1σ2CyB2A2D1yD2B1σx222221xyyxyxoxD1yyB2D2CA1σ1A2σ2主平面方位αo2由CD1顺时针转α2o到CA1所以从x轴顺时针转αo（负值）即到1对应的主平面的外法线αo确定后，1对应的主平面方位即确定。B1σx)(2)2(1110yxxCBDBtgyD2oyB2Cσ2αo2B1xD1A1σ1A2σx由此可定出主应力1所在平面的位置。由于A1A2为应力圆的直径,则2所在的另一主平面与1所在的主平面垂直。再根据应力圆判断α0的合理范围例题7-1从水坝体内某点处取出的单元体如图所示,x=-1MPa,y=-0.4MPa,x=-0.2MPa,y=0.2MPa,（1）绘出相应的应力圆（2）确定此单元体在=30°和=-40°两斜面上的应力。σxτxσyτyτyσyσxτxx1σx20.τx40.σy20.τyOB1B2D2(-0.4,0.2)D1(-1,-0.2)C解:(1)画应力圆OB2=y=-0.4MPa和B2D2=y=0.2MPa,定出D2点.OB1=x=-1MPa,B1D1=x=-0.2MPa,定出D1点;以D1D2为直径绘出的圆即为应力圆。将半径CD1逆时针转动逆时针转动22=60°=60°到半径CE,E点的坐标就代表=30°斜截面上的应力。(2)确定=30°斜截面上的应力oB1D1(-1,0.2)B2D2(-0.4,0.2)CEE600σ300τ300MPa680300.σMPa360300.τ(3)确定=-40°斜截面上的应力将半径CDCD11顺时针转顺时针转22=80°=80°到半径CF,F点的坐标就代表=-40°斜截面上的应力。oB1D1(-1,0.2)B2D2(-0.4,0.2)Cσ400τ400MPa950400.σMPa260400.τ800FxyMPa680300.σMPa360300.τMPa950400.σMPa260400.τ300α400α例题7-2两端简支的焊接工字钢梁及其荷载如图a,b所示,梁的横截面尺寸示于图c中。试绘出截面c上a,b两点处的应力圆，并用应力圆求出这两点处的主应力。250KN1.6m2mABC(a)12015152709zab单位：mm(c)250KN1.6m2mABC+200KN50KN+80KM.m解:首先计算支反力,并作出梁的剪力图和弯矩图MC=80kN•mQC左=200kN12015152709zab单位：mm)(IyMZ)(*dQISZZmmIZ463310882701113001201212mmya135mmSza32560005715015120...