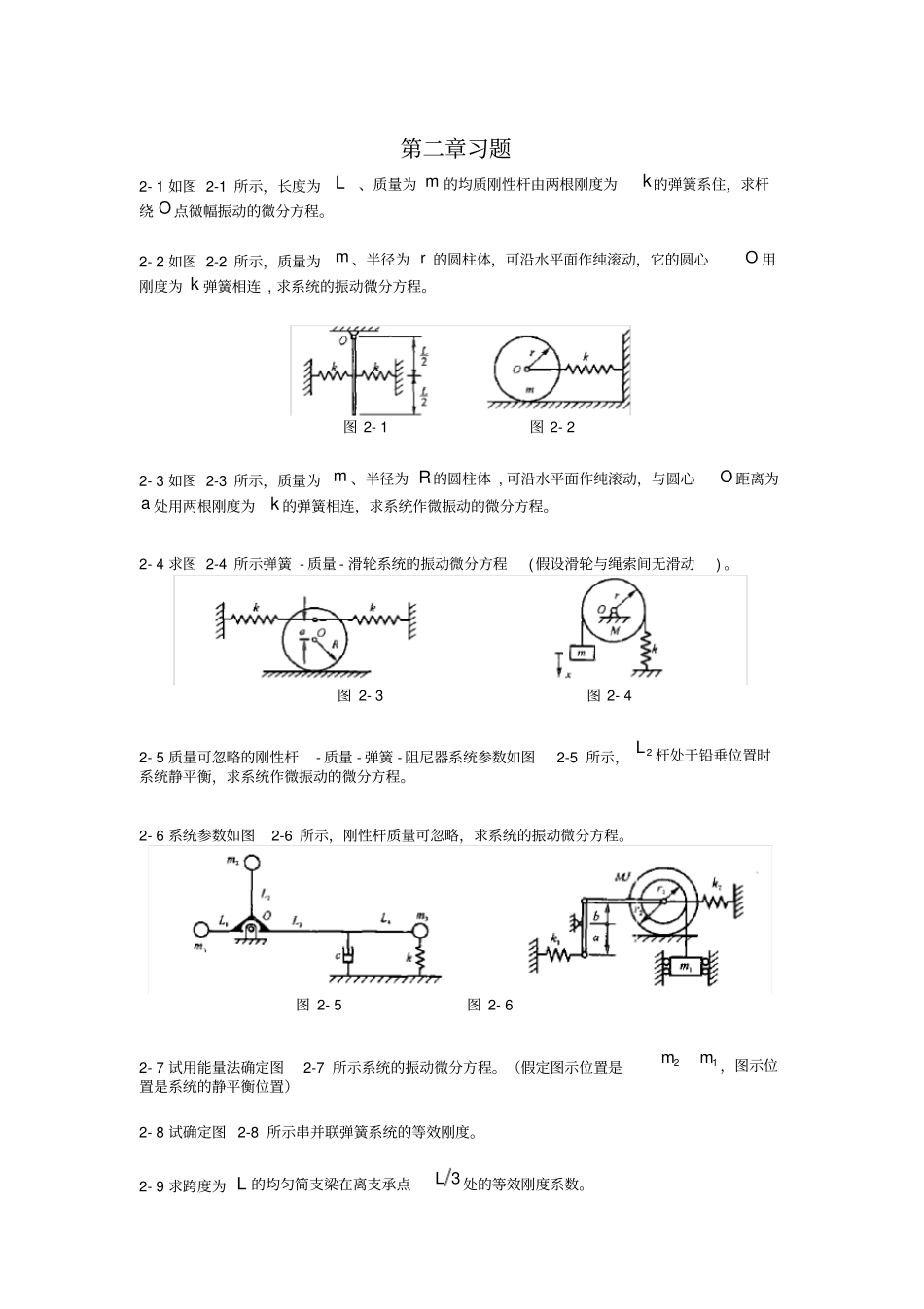
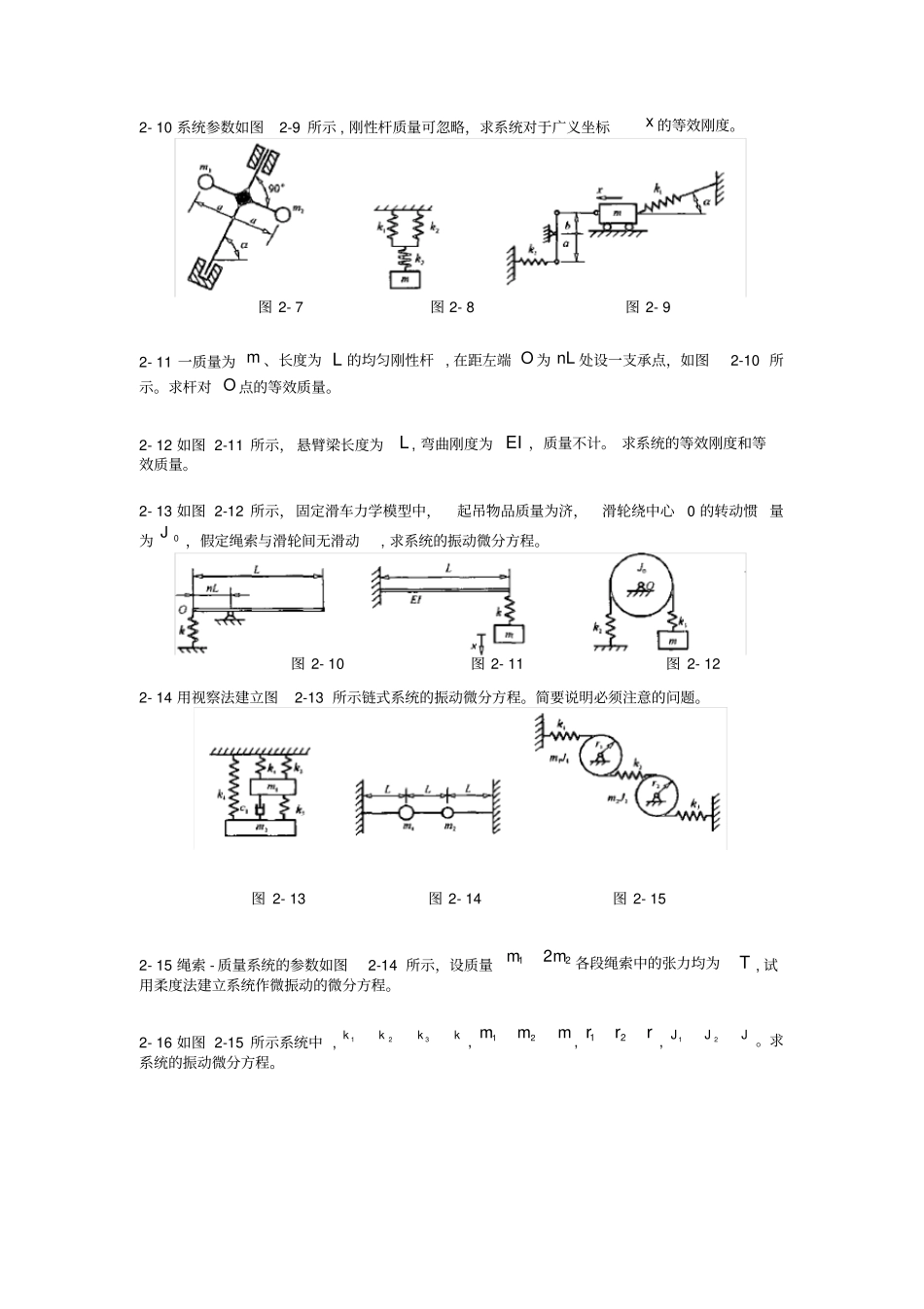
第二章习题2- 1 如图 2-1 所示,长度为L、质量为 m 的均质刚性杆由两根刚度为k的弹簧系住,求杆绕 O 点微幅振动的微分方程。2- 2 如图 2-2 所示,质量为m 、半径为 r 的圆柱体,可沿水平面作纯滚动,它的圆心O 用刚度为 k 弹簧相连 , 求系统的振动微分方程。2- 3 如图 2-3 所示,质量为 m 、半径为 R的圆柱体 , 可沿水平面作纯滚动,与圆心O 距离为a 处用两根刚度为k 的弹簧相连,求系统作微振动的微分方程。2- 4 求图 2-4 所示弹簧 - 质量 - 滑轮系统的振动微分方程(假设滑轮与绳索间无滑动) 。2- 5 质量可忽略的刚性杆- 质量 - 弹簧 - 阻尼器系统参数如图2-5 所示,2L 杆处于铅垂位置时系统静平衡,求系统作微振动的微分方程。2- 6 系统参数如图2-6 所示,刚性杆质量可忽略,求系统的振动微分方程。2- 7 试用能量法确定图2-7 所示系统的振动微分方程。(假定图示位置是21mm ,图示位置是系统的静平衡位置)2- 8 试确定图 2-8 所示串并联弹簧系统的等效刚度。2- 9 求跨度为 L 的均匀简支梁在离支承点3L处的等效刚度系数。图 2- 1 图 2- 2 图 2- 3 图 2- 4 图 2- 5 图 2- 6 2- 10 系统参数如图2-9 所示 , 刚性杆质量可忽略,求系统对于广义坐标x 的等效刚度。2- 11 一质量为 m 、长度为 L 的均匀刚性杆 , 在距左端 O 为 nL 处设一支承点,如图2-10 所示。求杆对 O 点的等效质量。2- 12 如图 2-11 所示, 悬臂梁长度为L , 弯曲刚度为 EI ,质量不计。 求系统的等效刚度和等效质量。2- 13 如图 2-12 所示,固定滑车力学模型中,起吊物品质量为济,滑轮绕中心0 的转动惯 量为0J,假定绳索与滑轮间无滑动, 求系统的振动微分方程。2- 14 用视察法建立图2-13 所示链式系统的振动微分方程。简要说明必须注意的问题。2- 15 绳索 - 质量系统的参数如图2-14 所示,设质量122mm 各段绳索中的张力均为T , 试用柔度法建立系统作微振动的微分方程。2- 16 如图 2-15 所示系统中 ,123kkkk ,12mmm ,12rrr ,12JJJ 。求系统的振动微分方程。图 2- 7图 2- 8图 2- 9 图 2- 10图 2- 11图 2- 12图 2- 13图 2- 14图 2- 152- 17 行车载重小车运动的力学模型如图2-16 所示,小车质量为1m ,所受到两根刚度为k 弹簧的约束, 悬挂物品质量为2m,悬挂长度为 L摆角很小 , 求系统的振动微分方程。2-...