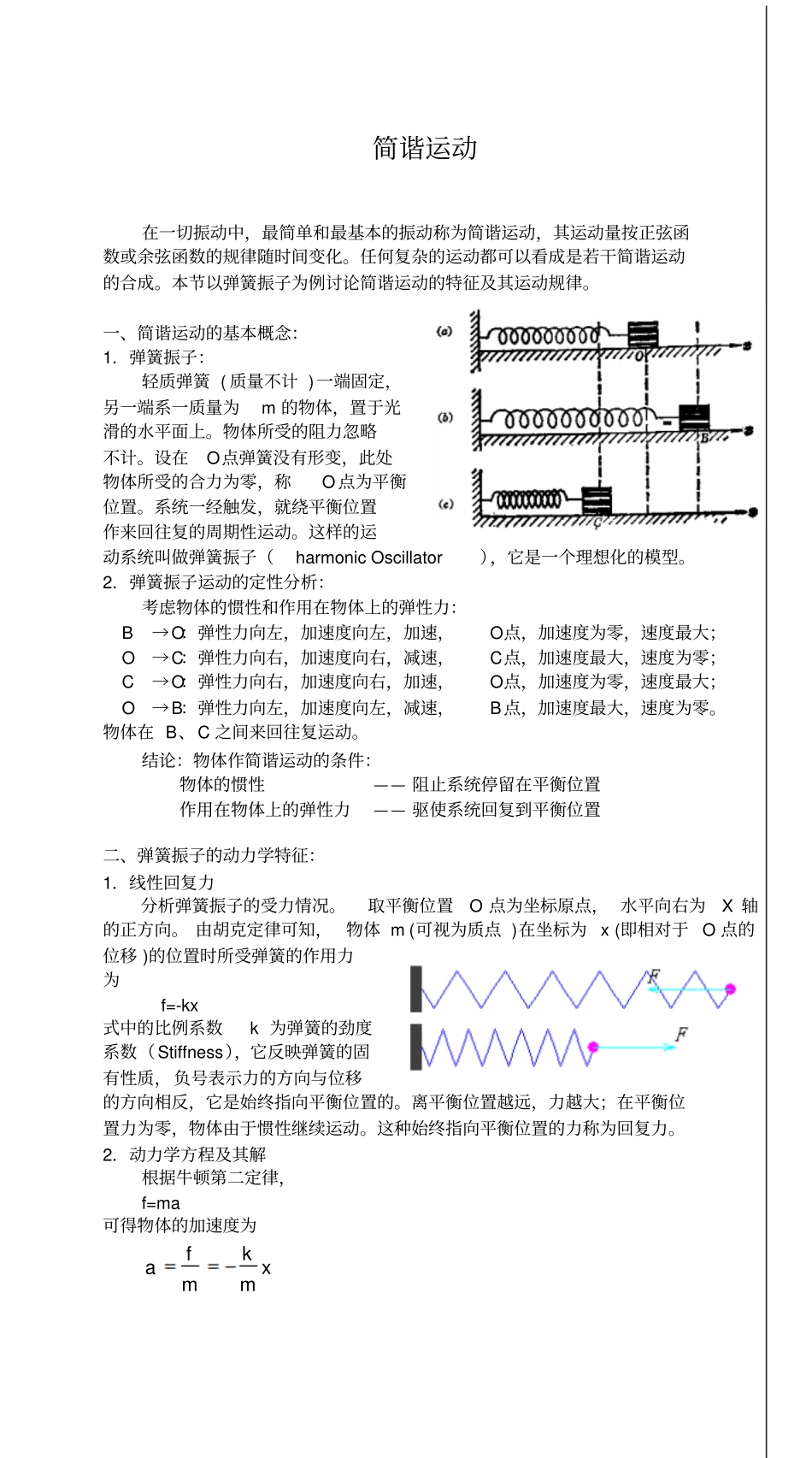
简谐运动在一切振动中,最简单和最基本的振动称为简谐运动,其运动量按正弦函数或余弦函数的规律随时间变化。任何复杂的运动都可以看成是若干简谐运动的合成。本节以弹簧振子为例讨论简谐运动的特征及其运动规律。一、简谐运动的基本概念:1.弹簧振子:轻质弹簧 ( 质量不计 )一端固定,另一端系一质量为m 的物体,置于光滑的水平面上。物体所受的阻力忽略不计。设在O点弹簧没有形变,此处物体所受的合力为零,称O 点为平衡位置。系统一经触发,就绕平衡位置作来回往复的周期性运动。这样的运动系统叫做弹簧振子(harmonic Oscillator),它是一个理想化的模型。2.弹簧振子运动的定性分析:考虑物体的惯性和作用在物体上的弹性力: B→O:弹性力向左,加速度向左,加速,O点,加速度为零,速度最大; O→C:弹性力向右,加速度向右,减速,C点,加速度最大,速度为零; C→O:弹性力向右,加速度向右,加速,O点,加速度为零,速度最大; O→B:弹性力向左,加速度向左,减速,B点,加速度最大,速度为零。物体在 B、C 之间来回往复运动。结论:物体作简谐运动的条件:物体的惯性—— 阻止系统停留在平衡位置作用在物体上的弹性力—— 驱使系统回复到平衡位置二、弹簧振子的动力学特征:1.线性回复力分析弹簧振子的受力情况。取平衡位置O 点为坐标原点, 水平向右为X 轴的正方向。 由胡克定律可知, 物体 m (可视为质点 )在坐标为 x (即相对于 O 点的位移 )的位置时所受弹簧的作用力为f=-kx 式中的比例系数k 为弹簧的劲度系数(Stiffness),它反映弹簧的固有性质,负号表示力的方向与位移的方向相反,它是始终指向平衡位置的。离平衡位置越远,力越大;在平衡位置力为零,物体由于惯性继续运动。这种始终指向平衡位置的力称为回复力。2.动力学方程及其解根据牛顿第二定律,f=ma 可得物体的加速度为xmkmfa机械振动 —— 简谐振动的基本概念1 对于给定的弹簧振子,m 和 k 均为正值常量,令mk=2则上式可以改写为xa2即xdtxd222或0222=+xdtxd这就是简谐运动的微分方程。三、简谐运动的运动学特征:1.简谐振动的表达式(运动学方程)简谐运动的微分方程的解具有正弦、余弦函数或指数形式。我们采用余弦函数形式,即)cos(tAx这就是简谐运动的运动学方程,式中A 和 φ 是积分常数。说明:1)简谐运动不仅是周期性的,而且是有界的, 只有正弦函数、 余弦函数或它们的组合才具有这种性质,这里我们采用余...