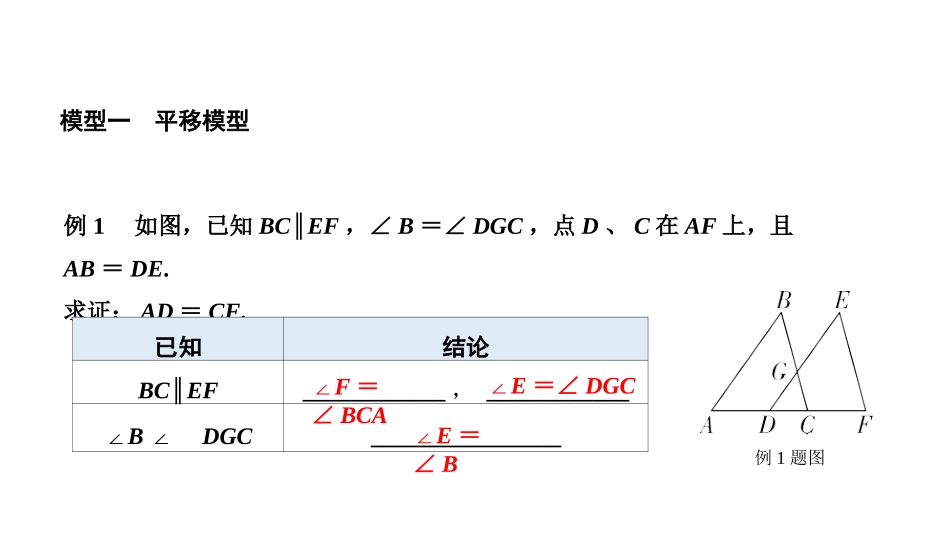
专题常见全等模型微专题五大常考全等模型模型一平移模型例1如图,已知BC∥EF,∠B=∠DGC,点D、C在AF上,且AB=DE.求证:AD=CF.已知结论BC∥EF____________,____________∠B∠DGC________________∠F=∠BCA∠E=∠DGC∠E=∠B例1题图证明: BC∥EF,∴∠F=∠BCA,∠E=∠DGC, ∠B=∠DGC,∴∠B=∠E,又 AB=DE,∴△ABC△DEF(AAS),∴AC=DF, AD+CD=CD+CF,∴AD=CF.≌【自主作答】基本模型图示模型总结有一组边共线或部分重合,另两组边分别平行,常要在移动方向上加(减)公共线段,构造线段相等,并利用平行线性质找到对应角相等1.如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.(1)求证:△AED△EBC;≌(1)证明: AD∥EC,∴∠A=∠BEC, E是AB的中点,∴AE=EB, ∠AED=∠B,∴△AED△EBC;≌(2)解: △AED△EBC,∴AD=EC,又 AD∥EC,∴四边形AECD是平行四边形,∴CD=AE, AB=6,AE=AB,∴CD=AB=3.(2)当AB=6时,求CD的长.1212≌模型二轴对称模型例2如图,在△ABC中,AB=AC,点D是三角形内一点,连接DA,DB,DC,若∠1=∠2,则△ABD与△ACD全等吗?请说明理由.已知结论AB=AC__________________∠1=∠2DB=DC,________________∠ABC=∠ACB∠ABD=∠ACD例2题图【自主作答】解:△ABD与△ACD全等.理由: ∠1=∠2,∴DB=DC. AB=AC,∴∠ABC=∠ACB.∴∠ABC-∠1=∠ACB-∠2,∴∠ABD=∠ACD,在△ABD和△ACD中,AB=AC∠ABD=∠ACDBD=CD,∴△ABD△ACD(SAS).≌基本模型图示模型总结所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等第2题图2.如图,点E、F在BC上,AB=DC,∠B=∠C,请补充一个条件:__________________________________________________,使△ABF△DCE.≌(或BF=EC或∠A=∠D或∠AFB=∠DEC)BE=CF模型三一线三等角型(K型)例3如图,B、C、D三点在同一直线上,∠B=∠D=∠ACE,AB=CD.求证:△ABC△CDE.≌【分析】已知∠B=∠D,AB=CD,要证△ABC△CDE,只需证明∠A=∠DCE即可.例3题图≌证明: ∠B=∠D=∠ACE,∠ACE+∠ACB+∠DCE=180°,∠B+∠ACB+∠A=180°,∴∠A=∠DCE,在△ABC和△CDE中,【自主作答】∠B=∠DAB=CD∠A=∠DCE,∴△ABC△CDE(ASA).≌图示模型总结三个等角(∠A=∠CPD=∠B)在同一直线上,称一线三等角模型(角度有锐角、钝角,若等角为直角称一线三垂直(见拓展模型),利用三等角和三角形内角和找全等三角形所需的角相等的条件为∠1=∠2.一线三等角的解题理念:有边相等证全等;无边相等证相似图示模型总结有三个直角,常利用同角(等角)的余角相等证明角相等3.如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且BP=CD,∠APD=∠B,若∠APB=120°,则∠CDP的度数为()A.30°B.60°C.120°D.150°第3题图C第4题图4.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为()A.(1,2.5)B.(1,1+)C.(1,3)D.(-1,1+)333C5.如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB,且BD=BE.求证:AC=AD+CE.第5题图证明: ∠DAB=∠DBE,∴∠ADB+∠ABD=∠CBE+∠ABD.∴∠ADB=∠CBE.在△ADB和△CBE中,∠ADB=∠CBE∠DAB=∠BCEDB=BE,∴△ADB△CBE(AAS).∴AD=CB,AB=CE.∴AC=BC+AB=AD+CE.≌模型四旋转模型类型一不共顶点旋转模型例4如图,点A、B、C、D在同一直线上,AE∥DF,CE∥BF,AB=CD.求证:△EAC△FDB.≌已知结论AE∥DF____________CE∥BF__________________AB=CDAB+BC=BC+CD______________⇨∠A=∠D∠ACE=∠DBFAC=BD例4题图图示模型总结所给图形是一个中心对称图形,一个三角形绕中心对称点旋转180°,则可得到另一个三角形,两三角形有一组边共线,构造线段相等,并利用平行线性质找到对应角相等类型二共顶点旋转模型(手拉手模型)例5如图,四边形ABCD中,点E为AD上一点,∠BAE=∠BCE=90°,且BC=CE,AB=DE.求证:△ABC△DEC.≌【分析】题干已知BC...