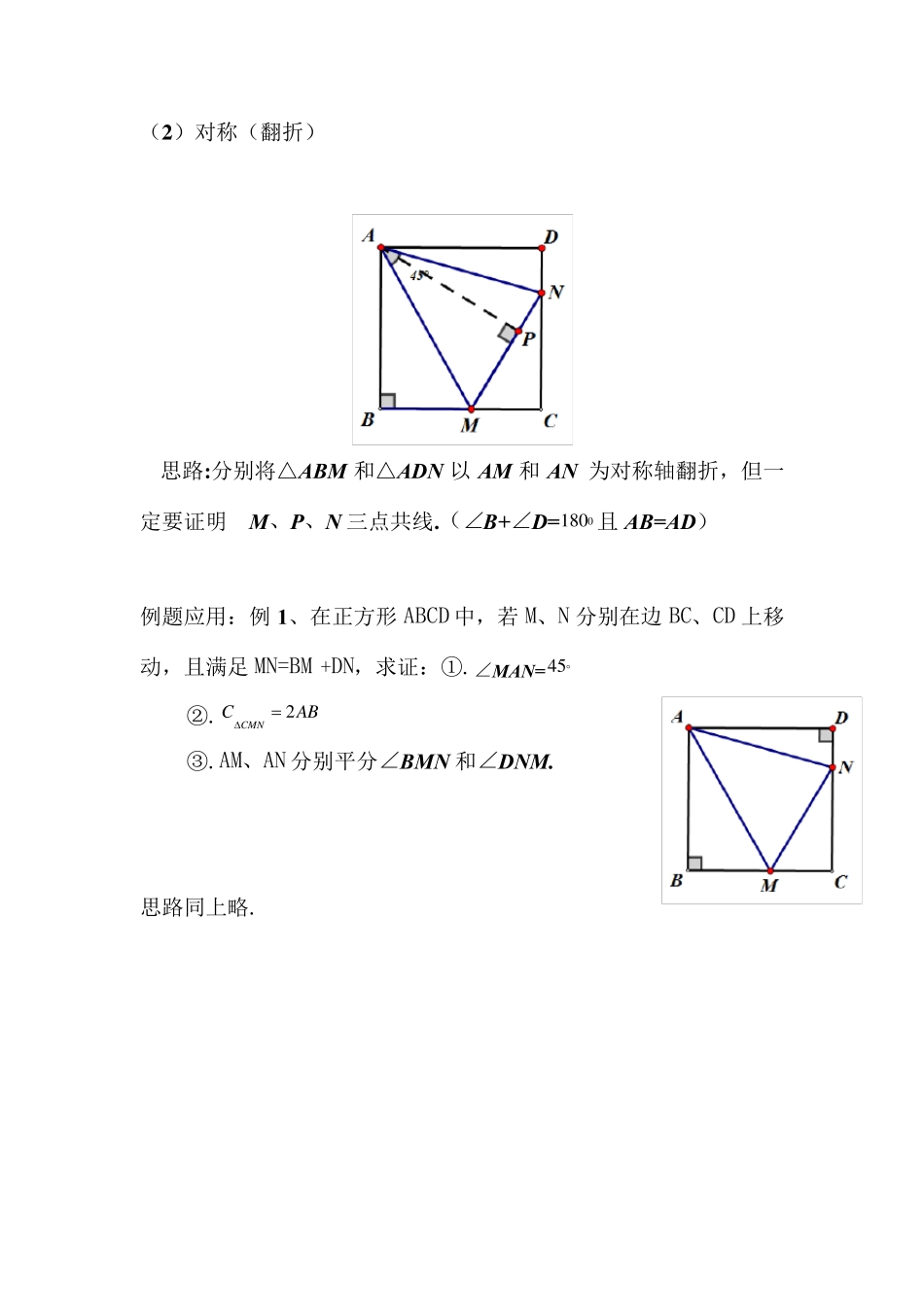
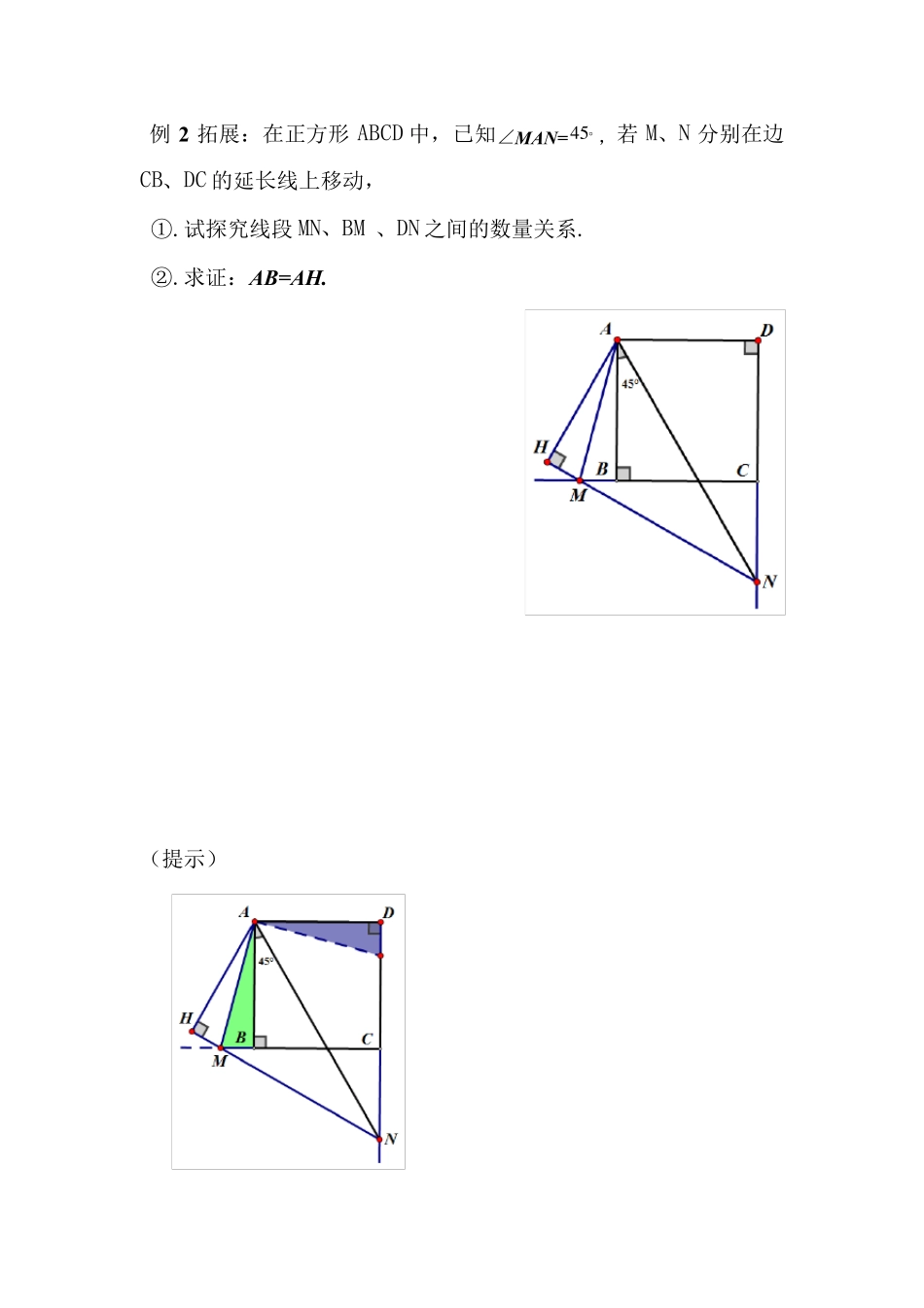
半角模型 过等腰△ABC(AB=AC)顶角A 引两条射线且它们的夹角为12∠A,这两条射线与底角顶点的相关直线交于M、N 两点,则BM、MN、NC 之间必然存在固定的关系,这种关系仅与两条相关直线及顶角A 相关 解决办法: 以A 为中心,把△CAN(顺时针或逆时针)旋转α度,至△ABN’,连接MN‘ 结论:1、△AMN≌△AMN’,MN=MN‘ 2、若BM、MN’、N‘B 共线,则存在x+y+z 型的关系 若不共线,则△BMN’中,∠MBN‘必与∠A 相关 应用环境: 1、顶角为特殊角的等腰三角形,如顶角为30°、45°、60°、75°90°,或它们的补角为这些特殊角度的时候; 2、正方形、菱形等也能产生等腰三角形 3、过底角顶点的两条相关直线:底边、底角两条角平分线、腰上的高、底角的邻补角的两条角平分线,底角的邻余角另外两边等;正方形或菱形的另外两边 4、此等腰三角形的相关弦 半角模型 条件: 思路:(1)、延长其中一个补角的线段 (延长 CD 到 E,使 ED=BM ,连AE 或延长 CB 到 F,使 FB=DN ,连AF ) 结论:①MN=BM+DN ② ③AM、AN 分别平分∠BMN和∠DNM .1 8 0210且ABCCMN2(2 )对称(翻折) 思路:分别将△ABM 和△ADN 以AM 和AN 为对称轴翻折,但一定要证明 M、P、N 三点共线.(∠B+∠D=且 AB=AD) 例题应用:例 1、在正方形 ABCD 中,若 M、N 分别在边 BC、CD 上移动,且满足 MN=BM +DN,求证:①.∠MAN= ②. ③.AM、AN 分别平分∠BMN 和∠DNM. 思路同上略. 01 8 04 5ABCCMN2 例2 拓展:在正方形ABCD 中,已知∠MAN=,若 M、N 分别在边CB、DC 的延长线上移动, ①.试探究线段 MN、BM 、DN 之间的数量关系. ②.求证:AB=AH. (提示) 4 5例3.在四边形ABCD 中,∠B+∠D=,AB=AD,若 E、F 分别在边BC、CD 上,且满足 EF=BE +DF.求证: (提示) 1 8 0.21BADEAF 例4,在△ABC 中,AB=AC,∠BAC=2∠DAE=120°,若 BD=5,CE=8,求 DE。 例五.请阅读下列材料: 已知:如图 1 在Rt ABC中, 90BAC ,ABAC,点 D 、E分别为线段 BC 上两动点,若45DAE.探究线段 BD 、 DE 、 EC 三条线段之间的数量关系. 小明的思路是:把AEC绕点 A顺时针旋转 90 ,得到ABE,连结 ED , 使问题得到解决.请你参考小明的思路探究并解决下列问题: (1)猜想 BD 、DE 、EC 三条线段之间存在的数量...