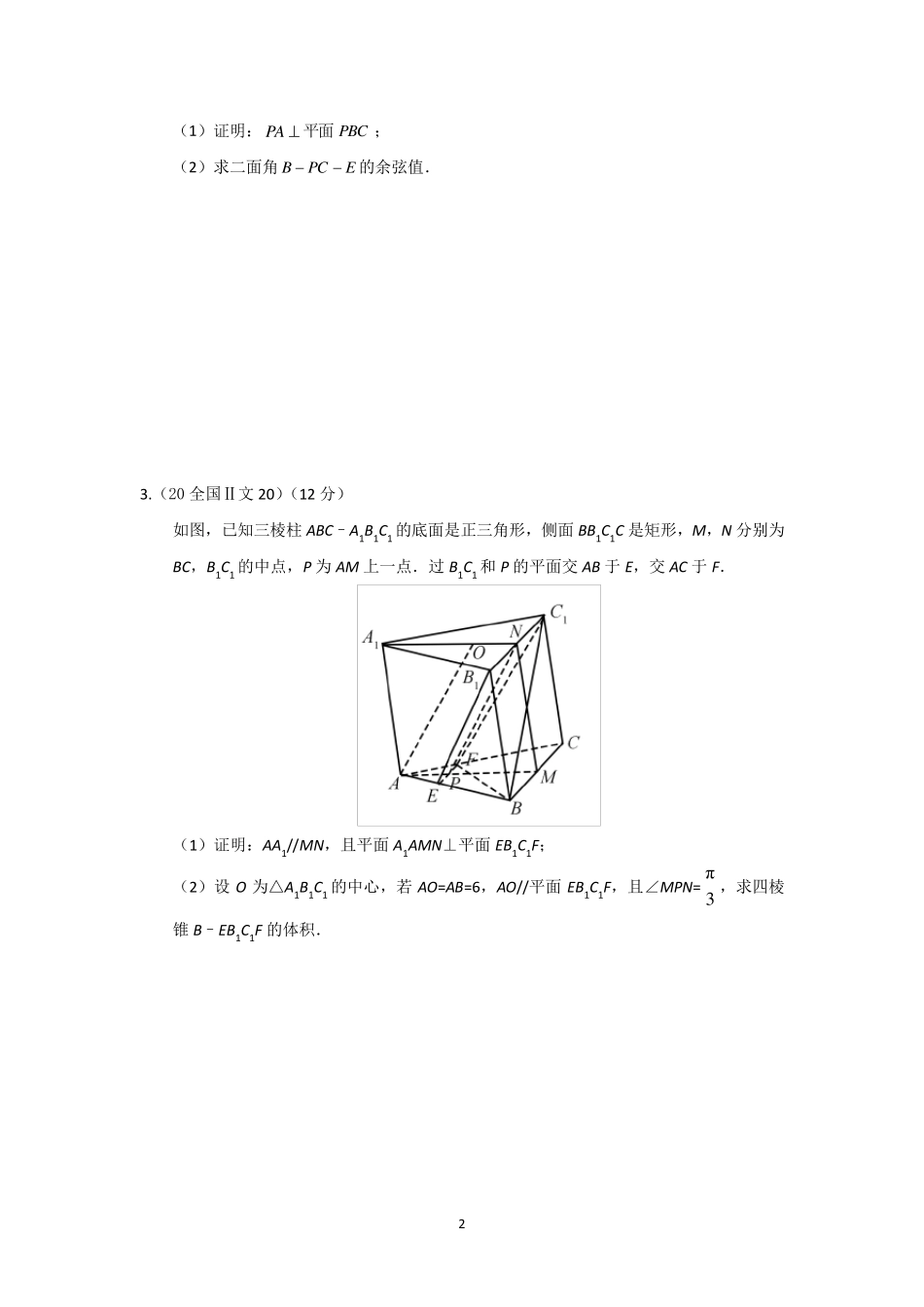
1 2020 年高考——立体几何 1.(20 全国Ⅰ文19) (12 分) 如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC△是底面的内接正三角形,P为DO上一点,∠APC=90°. (1)证明:平面PAB⊥平面PAC; (2)设 DO= 2 ,圆锥的侧面积为3π ,求三棱锥P−ABC 的体积. 2.(20 全国Ⅰ理 18)(12 分) 如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AEAD.ABC△是底面的内接正三角形,P为DO 上一点, 66PODO. 2 (1)证明:PA 平面PBC ; (2)求二面角BPCE的余弦值. 3.(20 全国Ⅱ文20)(12 分) 如图,已知三棱柱ABC–A1B1C1 的底面是正三角形,侧面BB1C1C 是矩形,M,N 分别为BC,B1C1 的中点,P为 AM 上一点.过 B1C1 和 P的平面交 AB 于 E,交 AC 于 F. (1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F; (2)设 O 为△A1B1C1 的中心,若 AO=AB=6,AO//平面EB1C1F,且∠MPN= π3 ,求四棱锥 B–EB1C1F 的体积. 3 4.(20 全国Ⅱ理 20)(12 分) 如图,已知三棱柱 ABC-A1B1C1 的底面是正三角形,侧面 BB1C1C 是矩形,M,N 分别为BC,B1C1 的中点,P为 AM 上一点,过 B1C1 和 P的平面交 AB 于 E,交 AC 于 F. (1)证明:AA1∥MN,且平面 A1AMN⊥EB1C1F; (2)设 O 为△A1B1C1 的中心,若 AO∥平面 EB1C1F,且 AO=AB,求直线 B1E 与平面 A1AMN所成角的正弦值. 5.(20 全国Ⅲ文 19)(12 分) 如图,在长方体1111ABCDA B C D中,点 E,F 分别在棱1DD ,1BB 上,且12DEED,12BFFB.证明: 4 (1 )当ABBC时,EFAC; (2 )点1C 在平面AEF 内. 6 .(20 全国Ⅲ理 1 9 )(1 2 分) 如图,在长方体1111ABCDA B C D中,点,E F 分别在棱11,DD BB 上,且12 DEED,12BFFB. (1 )证明:点1C 在平面AEF 内; (2 )若2AB ,1AD ,13AA ,求二面角1AEFA的正弦值. 5 7.(20新高考Ⅰ20)(12分) 如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l. (1)证明:l⊥平面PDC; (2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值. 6 8.(20 天津17)(本小题满分15 分) 如图,在三棱柱111ABCA B C中,1CC 平面,,2ABC ACBC ACBC,13CC ,点,DE 分别在棱1AA 和棱1CC 上,且2,...