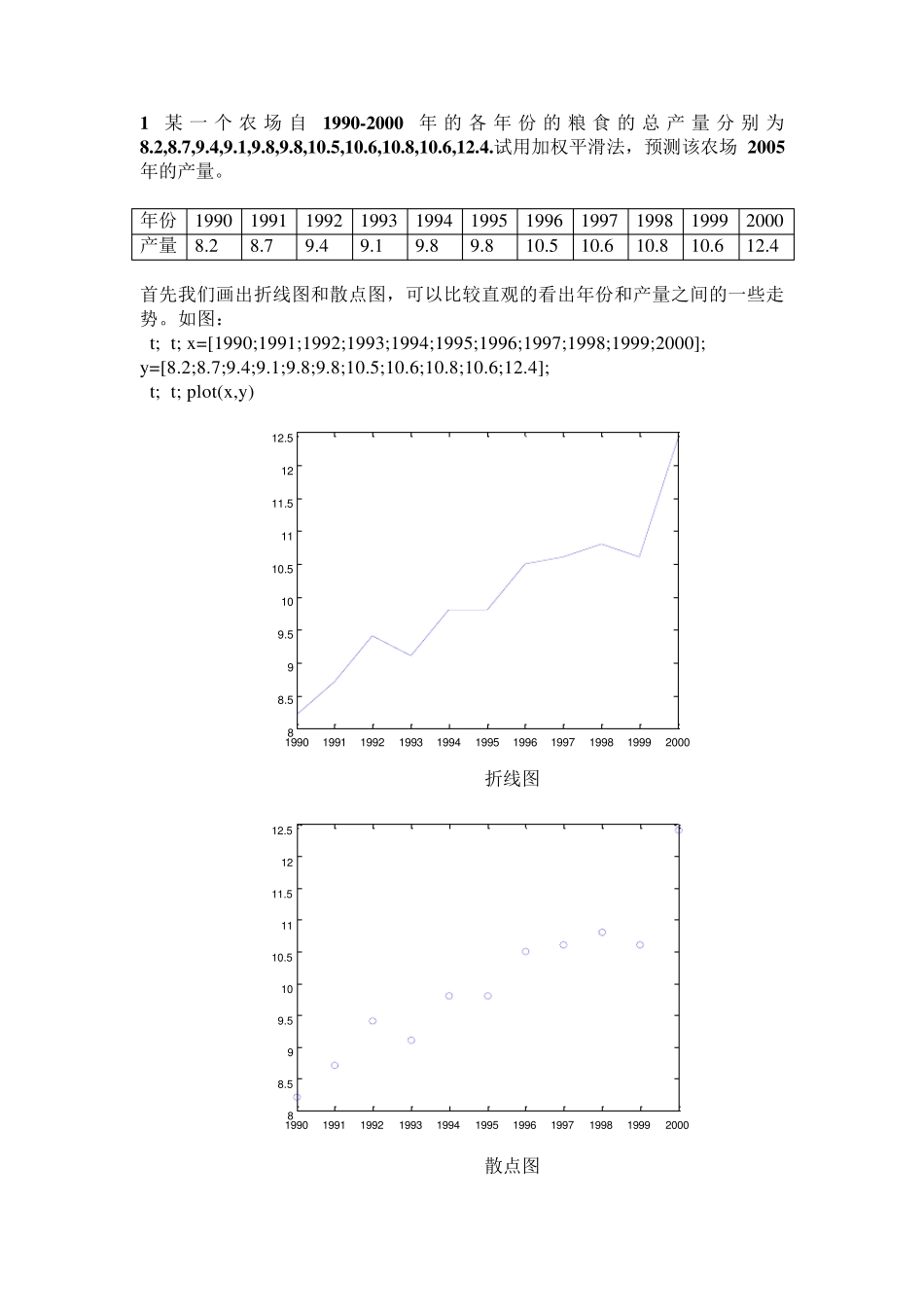
1某一个农场自1 9 9 0 -2 0 0 0年的各年份的粮食的总产量分别为8 .2 ,8 .7 ,9 .4 ,9 .1 ,9 .8 ,9 .8 ,1 0 .5 ,1 0 .6 ,1 0 .8 ,1 0 .6 ,1 2 .4 .试用加权平滑法,预测该农场2 0 0 5年的产量。 年份 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 产量 8.2 8.7 9.4 9.1 9.8 9.8 10.5 10.6 10.8 10.6 12.4 首先我们画出折线图和散点图,可以比较直观的看出年份和产量之间的一些走势。如图: >> x =[1990;1991;1992;1993;1994;1995;1996;1997;1998;1999;2000]; y =[8.2;8.7;9.4;9.1;9.8;9.8;10.5;10.6;10.8;10.6;12.4]; >> plot(x ,y ) 1 9 9 01 9 9 11 9 9 21 9 9 31 9 9 41 9 9 51 9 9 61 9 9 71 9 9 81 9 9 92 0 0 088 .599 .51 01 0 .51 11 1 .51 21 2 .5 折线图 1 9 9 01 9 9 11 9 9 21 9 9 31 9 9 41 9 9 51 9 9 61 9 9 71 9 9 81 9 9 92 0 0 088 .599 .51 01 0 .51 11 1 .51 21 2 .5 散点图 从上面的图形可以看出我们得到的年份和产量间的关系符合直线关系,故我们采用3 次加权平滑法来处理相关数据。从图知道近期数据的变化趋势应在预测模型中得到从分的反应,加权系数应该取得大一点,这里我们取 0.3. 做 3 次加权平滑程序(加权系数去 0.3): close all clear,clc % 统计数据 实际值 arr = [8.2 8.7 9.4 9.1 9.8 9.8 10.5 10.6 10.8 10.6 12.4]'; [m,nn]=size(arr); alpha = 0.3; % 平滑常数的范围为[0,1] % 1 次指数平滑 s1 = zeros(m,1); s1(1,1) = arr(1,1); for i=2:m s1(i) = alpha*arr(i,1)+(1-alpha)*s1(i-1); end sx1 = s1 % 2 次指数平滑 s2 = zeros(m,1); s2(1,1) = arr(1,1); for i=2:m s2(i) = alpha*s1(i,1)+(1-alpha)*s2(i-1); end sx2 = s2 % 3 次指数平滑 s3 = zeros(m,1); s3(1,1) = arr(1,1); for i=2:m s3(i) = alpha*s2(i,1)+(1-alpha)*s3(i-1); end sx3 = s3 % 计算二次曲线中的参数 a = zeros(m,1); b = zeros(m,1); c = zeros(m,1); beta=alpha/(2*(1-alpha)*(1-alpha)); a = 3*sx1-3*sx2+sx3; b = beta*((6-5*alpha)*sx1-2*(5-4*alpha)*sx2+(4-3*alpha)*sx3); c = beta*alpha*(sx1-2*sx2+sx3); % 二次曲线模型...