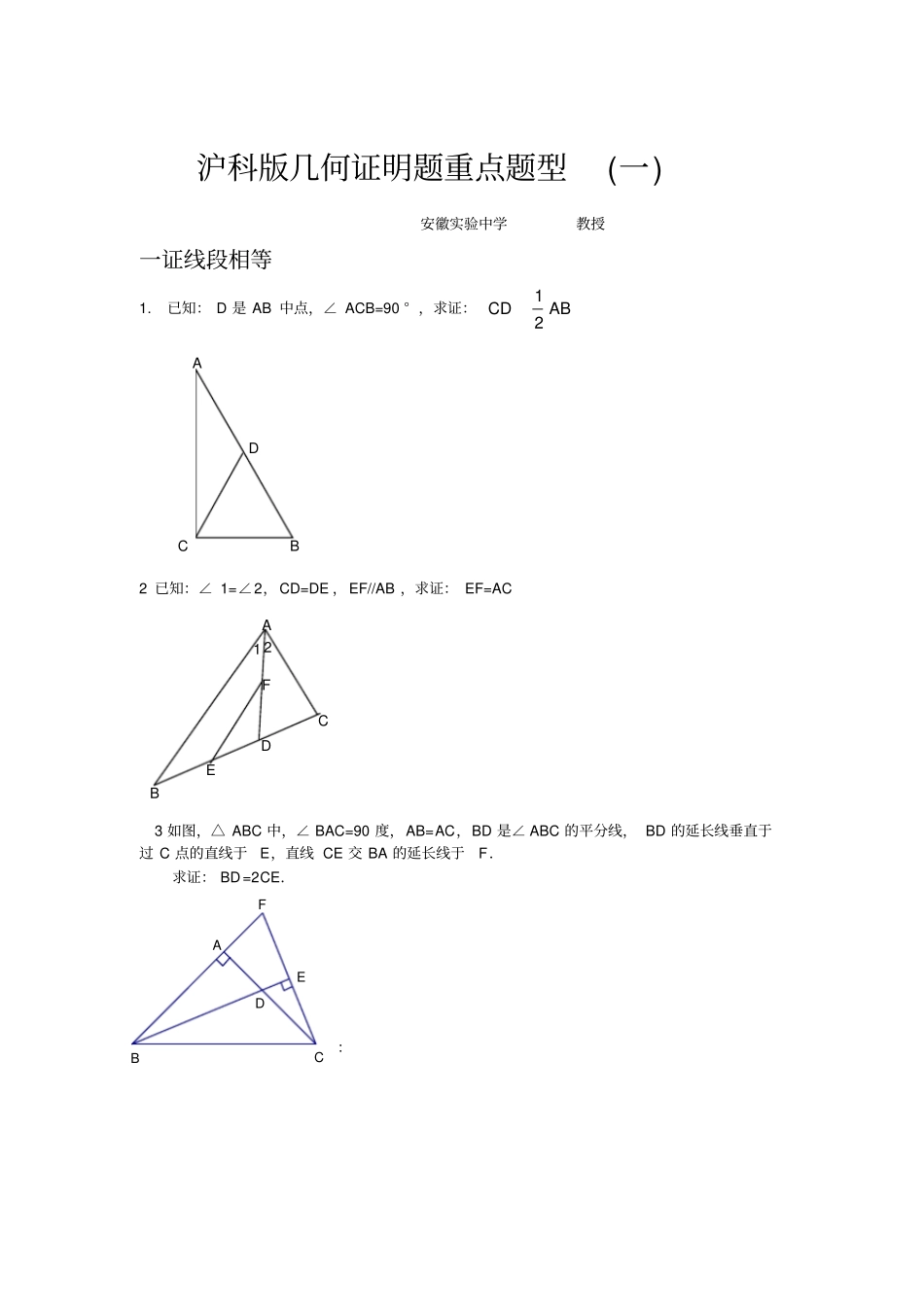
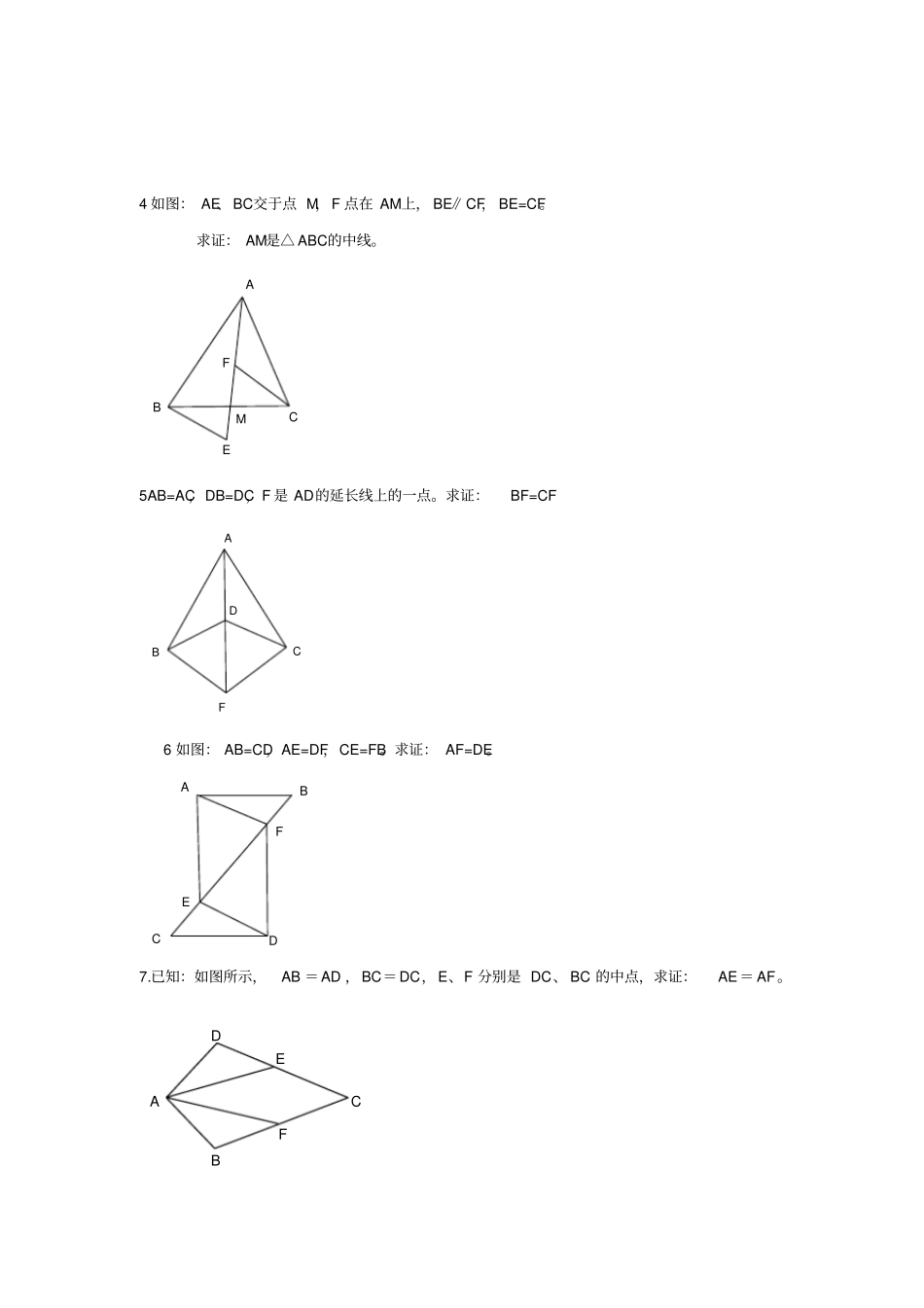
沪科版几何证明题重点题型(一)安徽实验中学教授一证线段相等1.已知: D 是 AB 中点,∠ ACB=90 ° ,求证:12CDAB2 已知:∠ 1=∠2,CD=DE ,EF//AB ,求证: EF=AC 3 如图,△ ABC 中,∠ BAC=90 度,AB=AC,BD 是∠ ABC 的平分线, BD 的延长线垂直于过 C 点的直线于E,直线 CE 交 BA 的延长线于F.求证: BD=2CE.:B A C D F 2 1 E D A B C FEDCBA4 如图: AE、BC交于点 M,F 点在 AM上, BE∥CF, BE=CF。求证: AM是△ ABC的中线。MFECBA5AB=AC,DB=DC,F 是 AD的延长线上的一点。求证:BF=CF FDCBA6 如图: AB=CD,AE=DF,CE=FB。求证: AF=DE。FEDCBA7.已知:如图所示,AB =AD ,BC=DC,E、F 分别是 DC、 BC 的中点,求证:AE= AF。D B CA F E 8.已知:如图, AB=AC,BDAC, CE AB,垂足分别为D、E,BD、CE 相交于点F,求证: BE=CD .9 如图,在△ ABC 中, AD 为∠ BAC 的平分线, DE⊥ AB 于 E,DF⊥AC 于 F。求证: DE=DF.10.如图: AB=AC ,ME ⊥AB , MF⊥AC ,垂足分别为E、F,ME=MF 。求证: MB=MC BCMAFE11.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF A E B M C F A E B D C F A C D E F 12 如图: BE ⊥AC ,CF⊥AB ,BM=AC ,CN=AB 。求证:(1)AM=AN ;(2)AM ⊥ AN。FBCAMNE123413 如图,已知AC ⊥AB , DB⊥AB ,AC =BE,AE =BD,试猜想线段CE 与 DE 的大小与位置关系,并证明你的结论. 14 如图,已知AB = DC,AC =DB ,BE=CE,求证: AE =DE. 15、如图 , 已知: AB⊥BC于 B , EF ⊥AC于 G , DF ⊥BC于 D , BC=DF.求证: AC=EF.16、已知:如图所示, BD为∠ ABC的平分线, AB=BC,点 P 在 BD上, PM⊥AD于 M,?PN⊥CD于 N,判断 PM与 PN的关系.A C E D B A B E C D FGEDCBAPDACBMN17、如图,△ ABC中,∠ BAC=90 度,AB=AC,BD是∠ ABC的平分线, BD的延长线垂直于过 C点的直线于 E,直线 CE交 BA的延长线于 F.求证: BD=2CE.、18 如图①, E、F 分别为线段 AC上的两个动点,且DE⊥AC于 E,BF⊥AC于 F,若 AB=CD,AF=CE,BD交 AC于点 M.i.求证: MB=MD,ME=MFii.当 E、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予...