中学数学竞赛中常用的几个重要定理

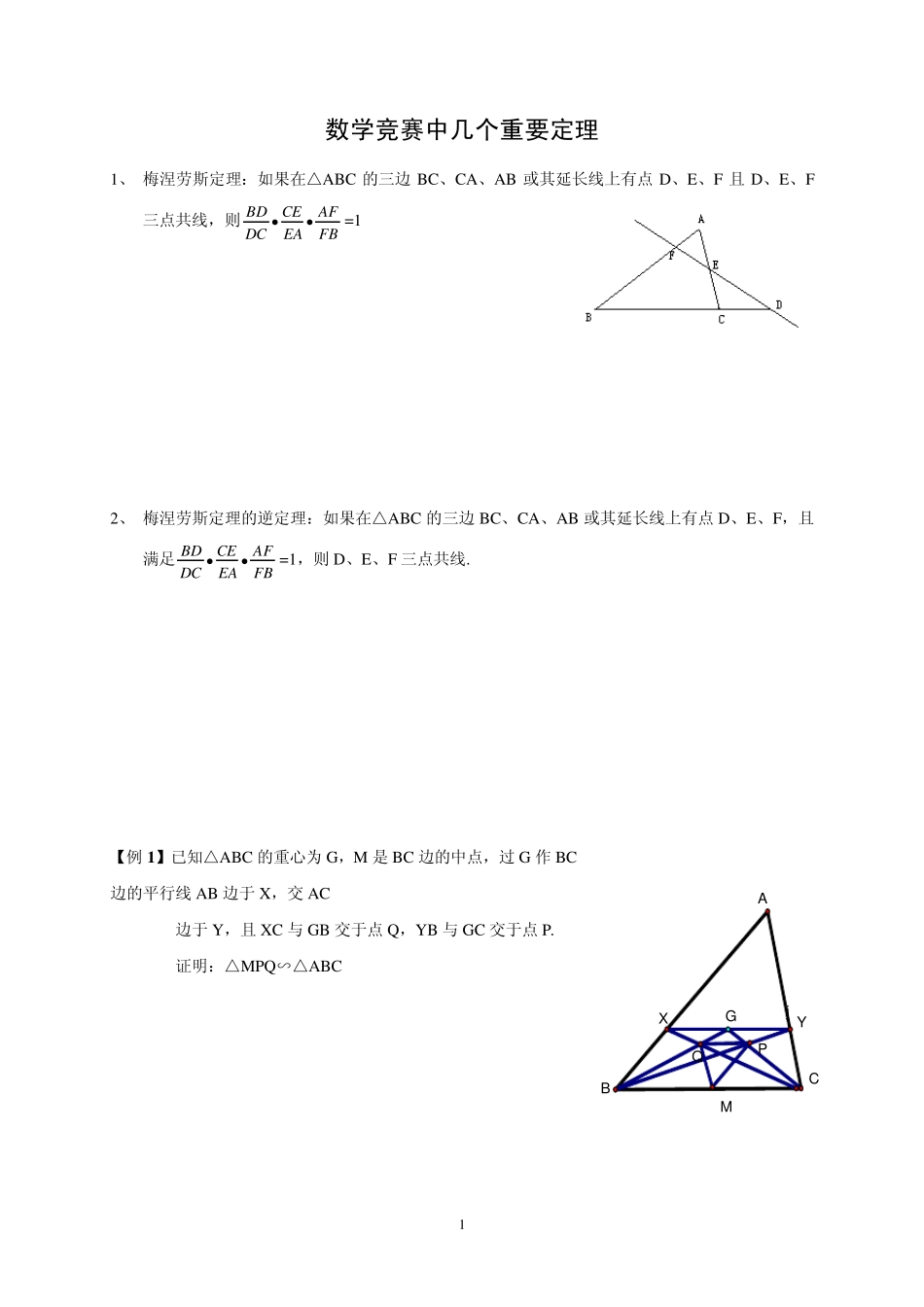
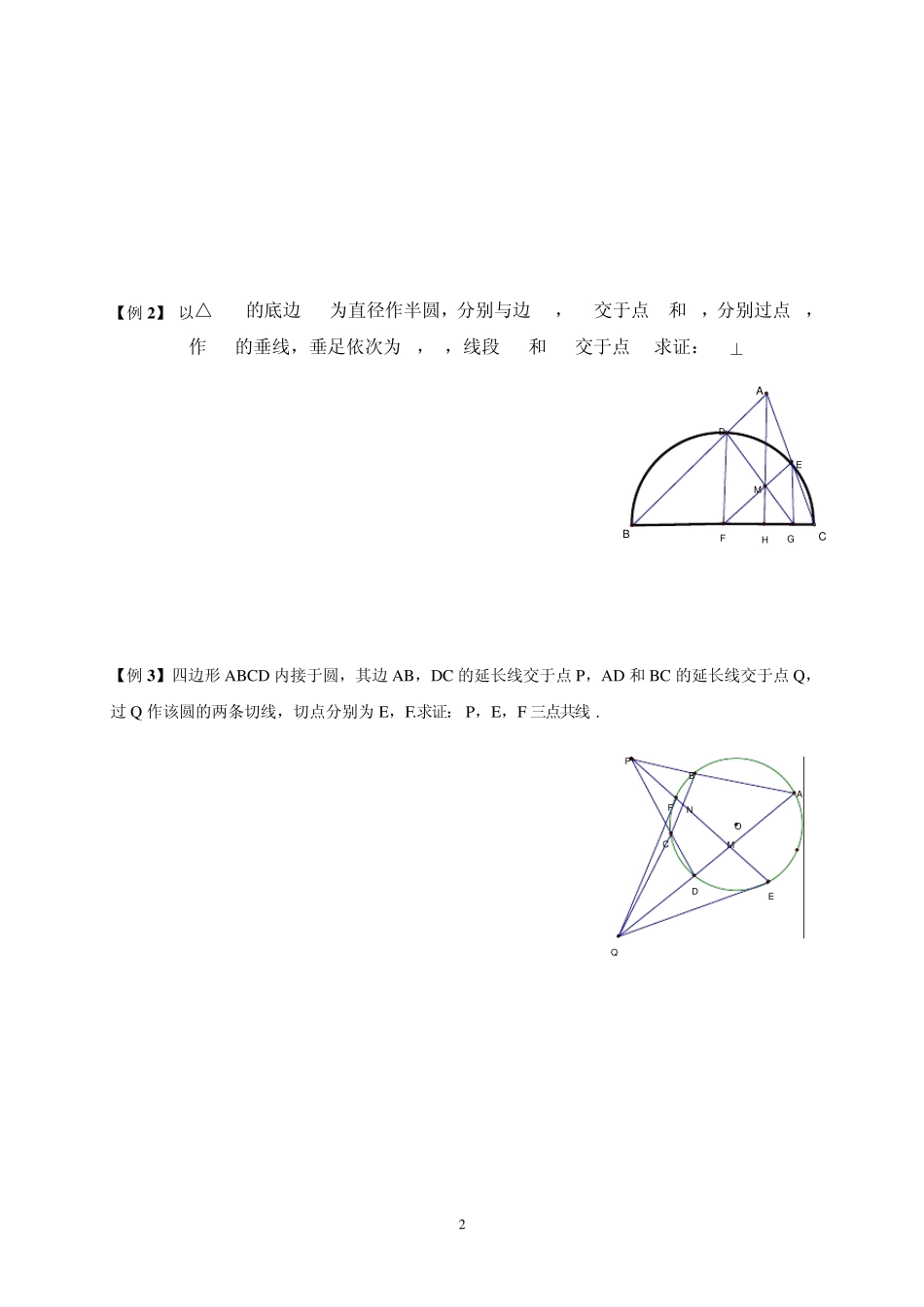
1 数学竞赛中几个重要定理 1、 梅涅劳斯定理：如果在△ABC 的三边BC、CA、AB 或其延长线上有点D、E、F 且D、E、F三点共线，则FBAFEACEDCBD=1 2、 梅涅劳斯定理的逆定理：如果在△ABC 的三边BC、CA、AB 或其延长线上有点D、E、F，且满足FBAFEACEDCBD=1，则D、E、F 三点共线. 【例1】已知△ABC 的重心为G，M 是BC 边的中点，过G 作BC边的平行线AB 边于X ，交AC 边于Y ，且X C 与GB 交于点Q ，Y B 与GC 交于点P. 证明：△MPQ ∽△ABC jMQGACBXYP 2 【例2】 以△ABC的底边BC为直径作半圆，分别与边AB，AC交于点D和E，分别过点D，E作BC的垂线，垂足依次为F，G，线段DG和EF交于点M.求证：AM⊥BC 【例3】四边形 ABCD 内接于圆，其边AB，DC 的延长线交于点P，AD 和BC 的延长线交于点Q ，过Q 作该圆的两条切线，切点分别为E，F.求证：P，E，F 三点共线. MDBFACHEGMNOQPBADCEF 3 【练习1 】设凸四边形ABCD 的对角线AC 和BD 交于点M，过M 作AD 的平行线分别交AB，CD于点E，F，交BC 的延长线于点O，P 是以O 为圆心，以OM 为半径的圆上一点. 求证：∠OPF=∠OEP 【练习2 】 在△ABC中，∠A=900，点D 在 AC 上，点E 在 BD 上，AE 的延长线交BC 于F. 若 BE：ED=2AC：DC，则∠ADB=∠FDC MBCDAEF0PEACBDF 4 塞瓦定理：设O 是△ABC 内任意一点，AO、BO、CO 分别交对边于N、P、M，则1PACPNCBNMBAM 塞瓦定理的逆定理： 设M、N、P分别在△ABC 的边AB、BC、CA 上，且满足1PACPNCBNMBAM，则AN、BP、CM 相交于一点. 【例1】B E 是△ABC 的中线，G 在BE 上，分别延长AG，CG 交BC，AB 于点D，F， 过D 作DN∥CG 交BG 于N，△DGL 及△FGM 是正三角形.求证：△LMN 为正三角形. GABCLMEDFN 5 【例2 】在△ABC 中，D 是BC 上的点DCBD = 31，E 是AC 中点.AD 与BE 交于O，CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比 【练习1 】设P 为△ABC 内一点，使∠BPA=∠CPA，G 是线段 AP 上的一点，直线 BG，CG 分别交边AC，AB 于E，F.求证：∠ BPF=∠CPE 【练习2 】 在△ABC 中，∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点，且 AD 平分∠BAC，过点D 作垂线 DP⊥AB 于P，DQ ⊥AC 于Q ，CP 于BQ 相交于K. 求证：AK⊥BC DAOCEFBCAPGEFKACBDPQ 6 托勒密定理：四边形ABCD 是圆内接四边形，则有AB·CD+AD·B...