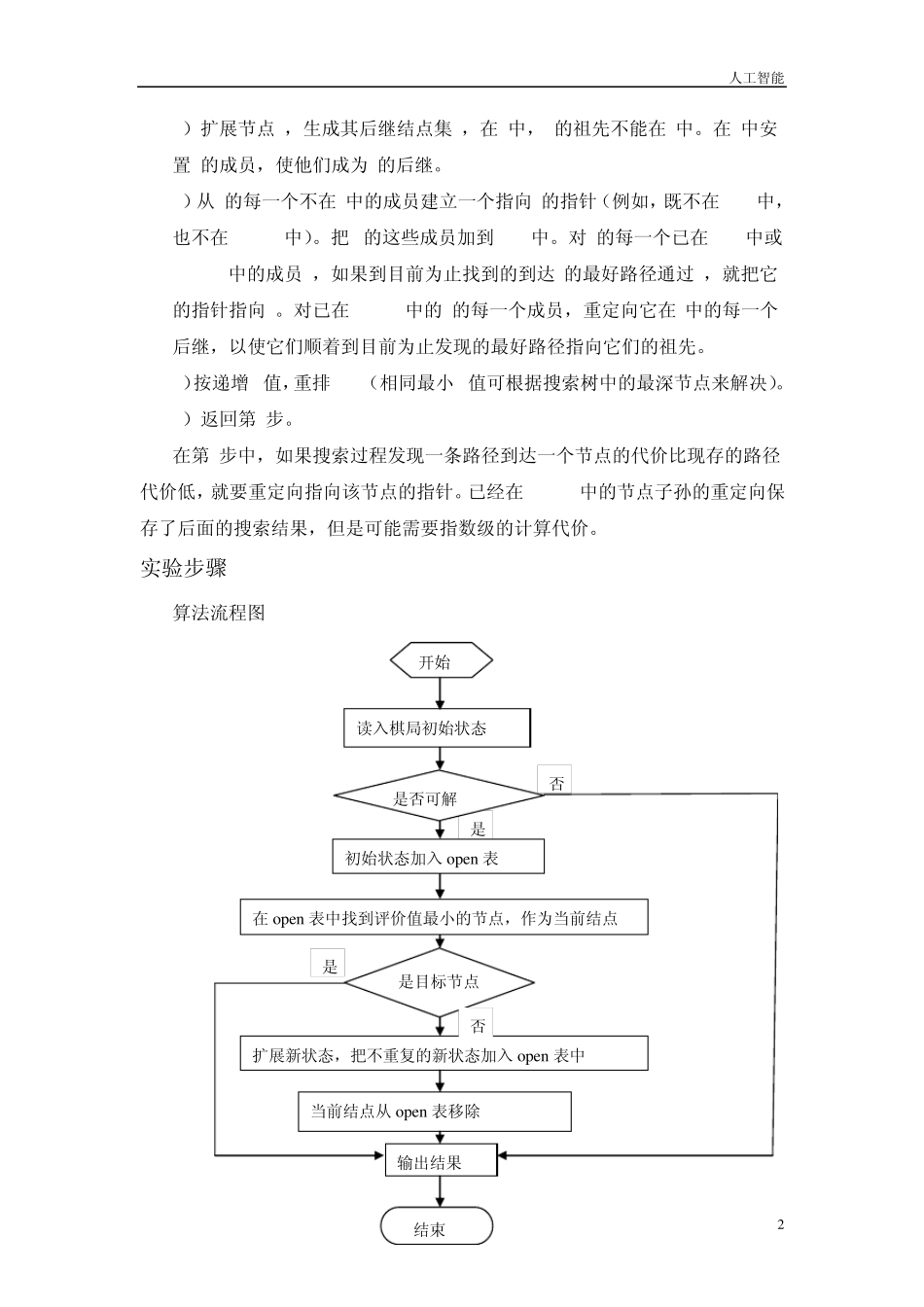
人工智能 1 A*算法实验报告 实验目的 1.熟悉和掌握启发式搜索的定义、估价函数和算法过程 2. 学会利用 A*算法求解 N 数码难题 3. 理解求解流程和搜索顺序 实验原理 A*算法是一种有序搜索算法,其特点在于对估价函数的定义上。对于一般的有序搜索,总是选择 f 值最小的节点作为扩展节点。因此,f 是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点 n 的估价函数值为两个分量:从起始节点到节点 n 的代价以及从节点 n 到达目标节点的代价。 实验条件 1. Window NT/xp/7 及以上的操作系统 2. 内存在 512M 以上 3. CPU 在奔腾 II 以上 实验内容 1. 分别以 8 数码和15 数码为例实际求解 A*算法 2. 画出 A*算法求解框图 3. 分析估价函数对搜索算法的影响 4. 分析 A*算法的特点 实验分析 1. A *算法基本步骤 1)生成一个只包含开始节点n0的搜索图G,把n0放在一个叫OPEN的列表上。 2)生成一个列表CLOSED,它的初始值为空。 3)如果OPEN表为空,则失败退出。 4)选择OPEN上的第一个节点,把它从OPEN中移入CLPSED,称该节点为n。 5)如果n是目标节点,顺着G中,从n到n0的指针找到一条路径,获得解决方案,成功退出(该指针定义了一个搜索树,在第7步建立)。 人工智能 2 6)扩展节点n,生成其后继结点集M,在G中,n的祖先不能在M中。在G中安置M的成员,使他们成为n的后继。 7)从M的每一个不在G中的成员建立一个指向n的指针(例如,既不在OPEN中,也不在CLOSED中)。把M1的这些成员加到OPEN中。对M的每一个已在OPEN中或CLOSED中的成员m,如果到目前为止找到的到达m的最好路径通过n,就把它的指针指向n。对已在CLOSED中的M的每一个成员,重定向它在G中的每一个后继,以使它们顺着到目前为止发现的最好路径指向它们的祖先。 8)按递增f*值,重排OPEN(相同最小f*值可根据搜索树中的最深节点来解决)。 9)返回第3步。 在第7步中,如果搜索过程发现一条路径到达一个节点的代价比现存的路径代价低,就要重定向指向该节点的指针。已经在CLOSED中的节点子孙的重定向保存了后面的搜索结果,但是可能需要指数级的计算代价。 实验步骤 算法流程图 是目标节点 是开始 读入棋局初始状态 是否可解 在open 表中找到评价值最小的节点,作为当前结点 初始状态加入 open 表 扩展新状态,把不重复的新状态加入 open 表中 当前结点从 open 表移除 输出结果 结...