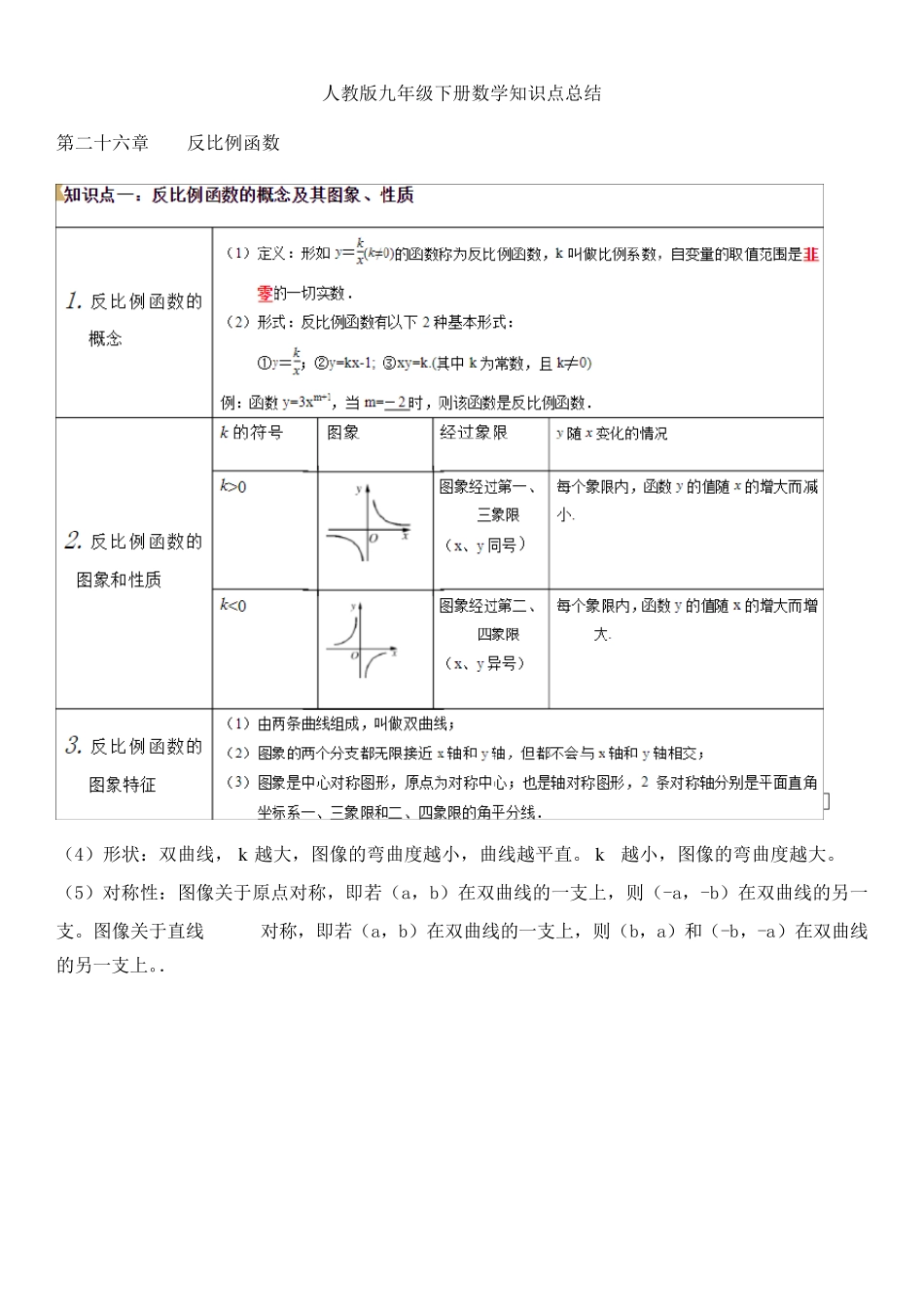
人教版九年级下册数学知识点总结 第二十六章 反比例函数 (4)形状:双曲线,k 越大,图像的弯曲度越小,曲线越平直。 k 越小,图像的弯曲度越大。 (5)对称性:图像关于原点对称,即若(a,b)在双曲线的一支上,则(-a,-b)在双曲线的另一支。图像关于直线对称,即若(a,b)在双曲线的一支上,则(b,a)和(-b,-a)在双曲线的另一支上。. 说明:(1)双曲线的两个分支是断开的,研究反比例函数的增减性时,要将两个分支分别讨论,不能一概而论。 (2)直线 与双曲线的关系: 当时,两图像没有交点;当时,两图像必有两个交点,且这两个交点关于原点成中心对称. 第二十七章 相似三角形 (①三边对应成比例②两个三角形的两个角对应相等;③两边对应成比例,且夹角相等;④相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比。) 7、相似三角形应用 视点:眼睛的位置;仰角:视线与水平线的夹角;盲区:看不到的区域。 知识点三 :位似 1.位似图形:如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行,那么这两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。 2.性质:在平面直角体系中,如果位似变换是以原点为位似中心,相似比为 k,那么位似图形的对应点的坐标的比等于 k 或-k。 注意 : 1、位似是一种具有位置关系的相似,所以两个图形是位似图形,必定是相似图形,而相似图形不一定是位似图形; 2、两个位似图形的位似中心只有一个; 3、两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧; 4、位似比就是相似比.利用位似图形的定义可判断两个图形是否位似; 5.位似图形的对应点和位似中心在同一直线上,它们到位似中心的距离之比等于相似比。位似多边形的对应边平行或共线。位似可以将一个图形放大或缩小。位似图形的中心可以在任意的一点,不过位似图形也会随着位似中心的位变而位变。 6.根据一个位似中心可以作两个关于已知图形一定位似比的位似图形,这两个图形分布在位似中心的两侧,并且关于位似中心对称。 第二十八章 锐角三角函数 补充:1、余切定义:在Rt△ABC中,锐角∠A的邻边与对边的比叫做∠A的余切,记作cotA,即cotA=∠A的邻边/∠A的对边=b/a; 2、一个锐角的正弦、余弦、正切、余切分别等于它的余角的余弦、正弦、余切、正切。(通常我们称正弦、余弦互为余函数。...