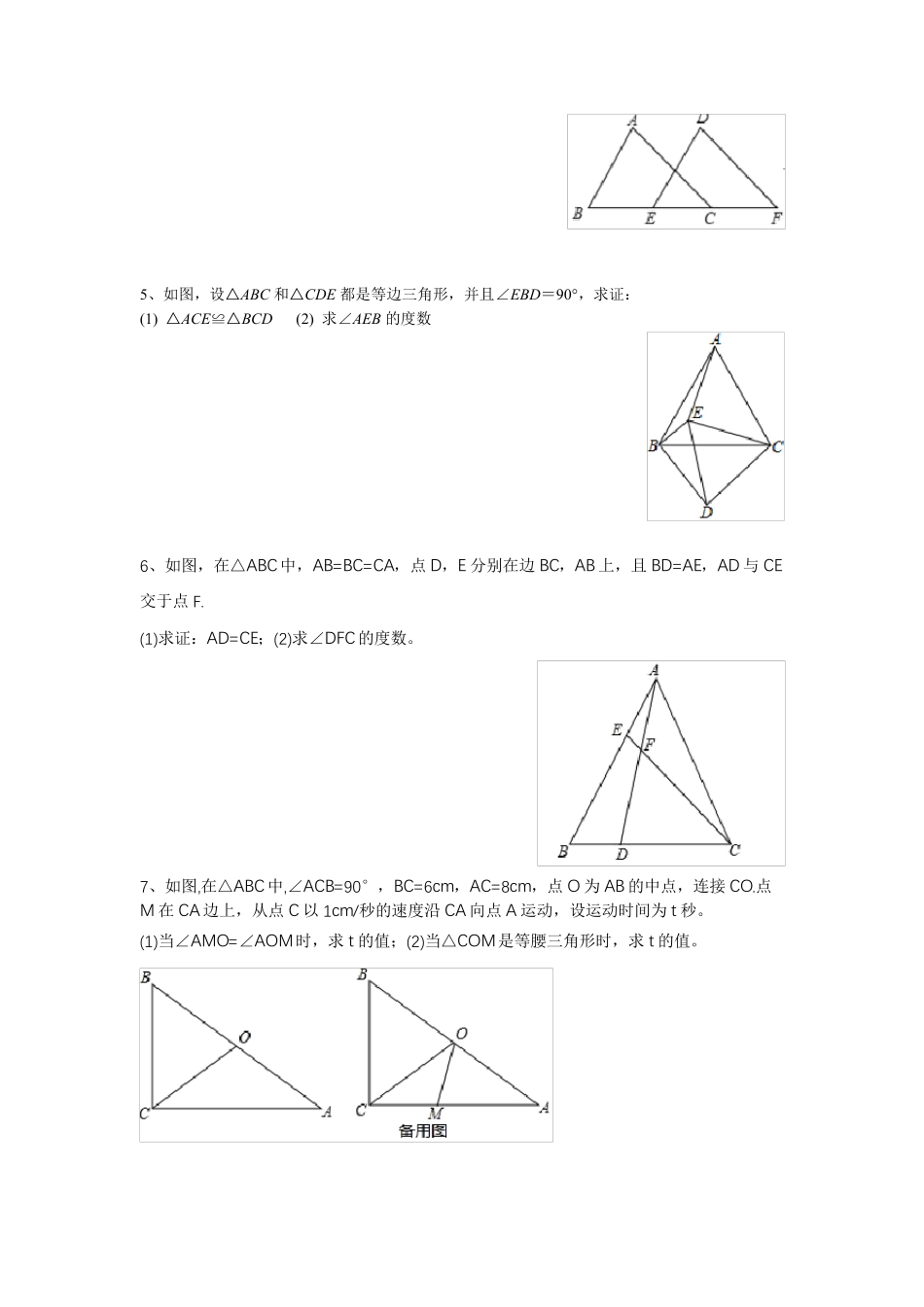
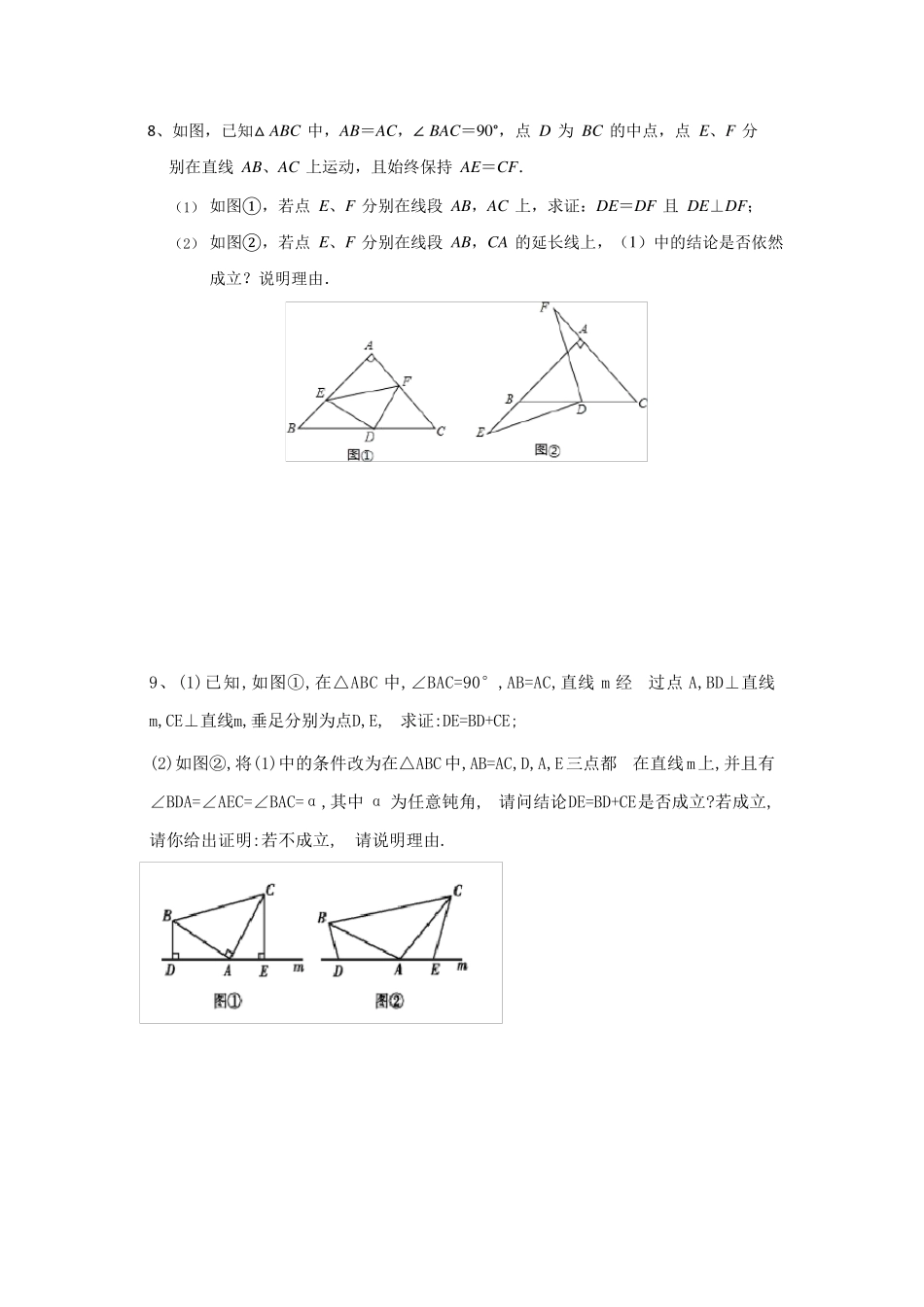
人教版八年级数学数学几何压轴题期末复习提高练习题 1、如图,在Rt△ABC 中,△ACB=90°,△A=40°,△ABC 的外角△CBD 的平分线BE 交AC 的延长线于点E. (1)求△CBE 的度数; (2)过点D 作DF∥BE,交AC 的延长线于点F,求△F 的度数. 2、如图,△ABC 中,AD⊥BC,EF 垂直平分AC,交AC 于点F,交BC 于点E,且BD=DE. (1)若∠BAE=40°,求∠C 的度数; (2)若△ABC 周长 13cm ,AC=6cm ,求 DC 长. 3、如图,在△ABC 中,△ABC=45°,CD△AB 于点D,AC 的垂直平分线BE 与 CD 交 于点F,与 AC 交于点E. (1)判断△DBC 的形状并证明你的结论. (2)求证:BF=AC. (3)试说明 CE= 21 BF. 4、如图,已知点B、E、C、F 在同一直线上,AB=DE,∠A=∠D,AC∥DF. 求证:(1)△ABC≌△DEF;(2)BE=CF. 5、如图,设△ABC 和△CDE都是等边三角形,并且∠EBD=90°,求证: (1) △ACE≌△BCD (2) 求∠AEB 的度数 6、如图,在△ABC中,AB=BC=CA,点D,E 分别在边BC,AB 上,且BD=AE,AD 与CE交于点F. (1)求证:AD=CE;(2)求∠DFC 的度数。 7、如图,在△ABC 中,∠ACB=90°,BC=6cm,AC=8cm,点O 为 AB 的中点,连接 CO.点M 在CA 边上,从点C 以 1cm/秒的速度沿 CA 向点A 运动,设运动时间为 t秒。 (1)当∠AMO=∠AOM时,求t的值;(2)当△COM是等腰三角形时,求t的值。 8、如图,已知△ ABC 中,AB=AC,∠ BAC=9 0 °,点 D 为 BC 的中点,点 E、F 分别在直线 AB、AC 上运动,且始终保持 AE=CF. (1) 如图① ,若点 E、F 分别在线段 AB,AC 上,求证:DE=DF 且 DE⊥DF; (2) 如图② ,若点 E、F 分别在线段 AB,CA 的延长线上,(1 )中的结论是否依然成立?说明理由. 9、(1)已知,如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经 过点 A,BD⊥直线 m,CE⊥直线 m,垂足分别为点 D,E, 求证:DE=BD+CE; (2)如图②,将(1)中的条件改为在△ABC 中,AB=AC,D,A,E 三点都 在直线 m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α 为任意钝角, 请问结论 DE=BD+CE 是否成立?若成立,请你给出证明:若不成立, 请说明理由. 10、如图,在 Rt△ABC 中,∠ACB=90°,AC=BC=4,CD⊥AB 于 D,P 是线段 CD 上一个动点,以 P 为直角顶点向下作等腰 Rt△BPE,连接 AE、DE. (1) ∠BAE 的度数是否为定值?若是,求...