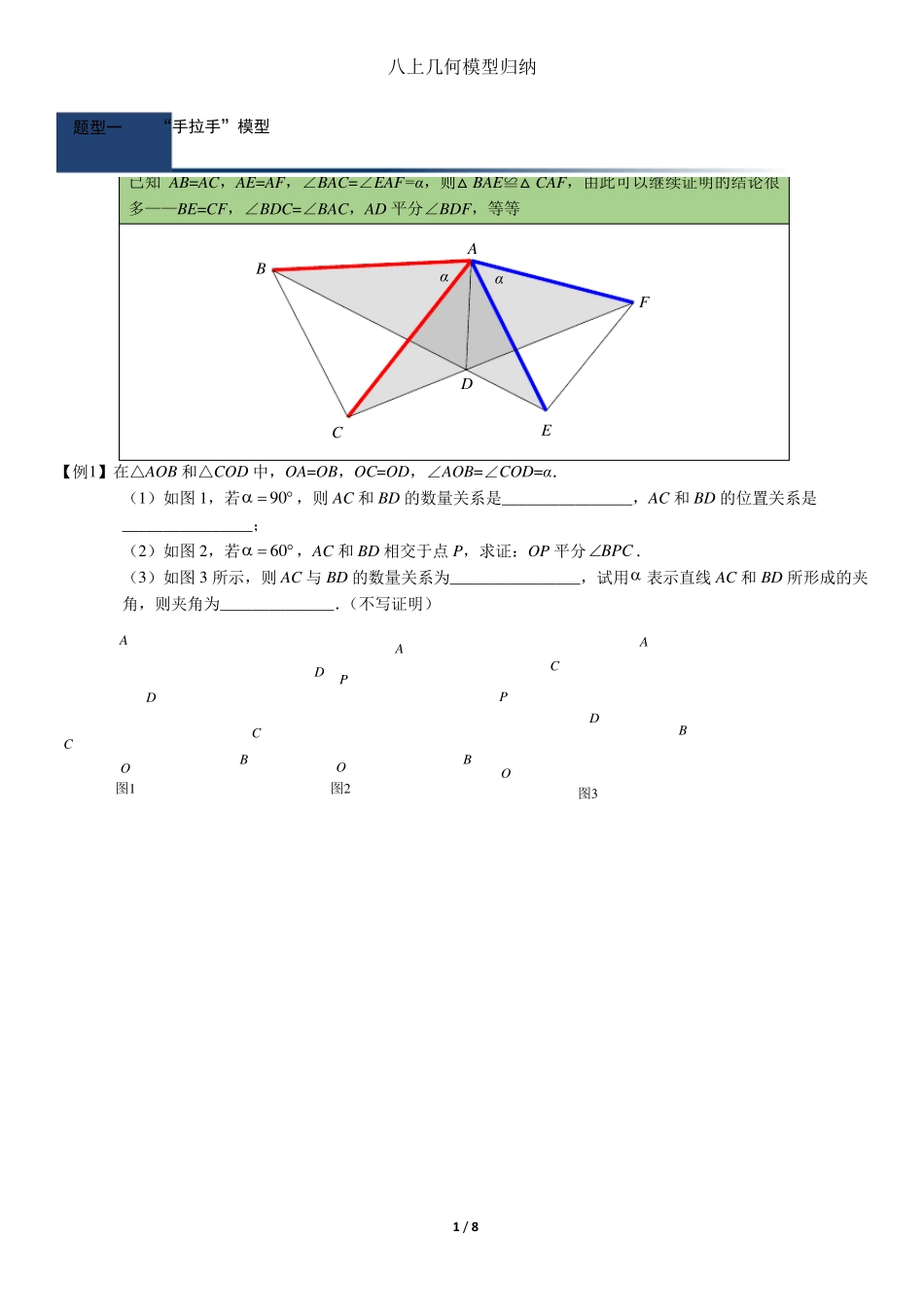
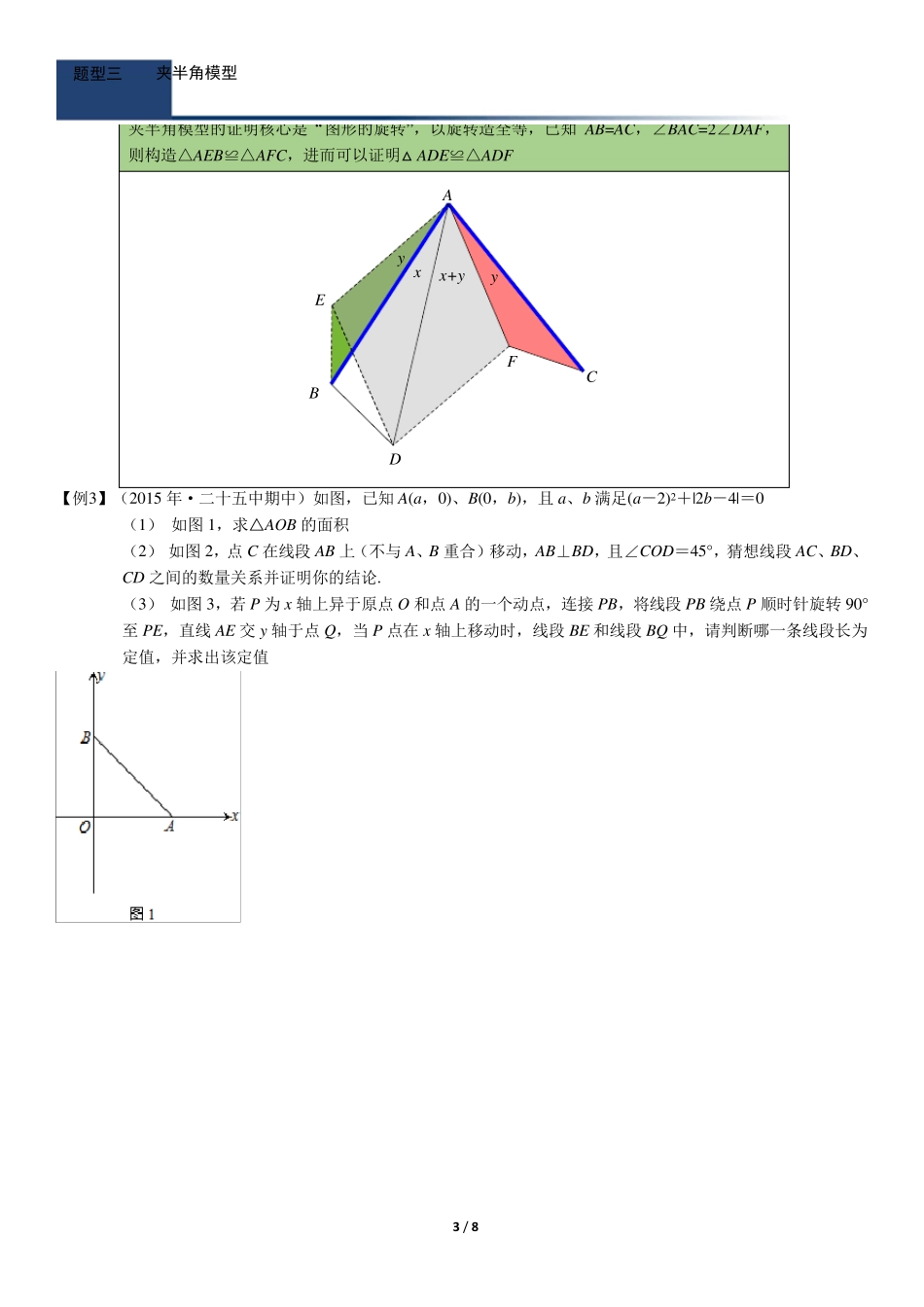
1 / 8 八上几何模型归纳 已知AB=AC,AE=AF,∠BAC=∠EAF=α,则△BAE≌△CAF,由此可以继续证明的结论很多——BE=CF,∠BDC=∠BAC,AD 平分∠BDF,等等 【例1】在△AOB 和△COD 中,OA=OB,OC=OD,∠AOB=∠COD=α. (1)如图 1,若,则AC 和 BD 的数量关系是________________,AC 和 BD 的位置关系是________________; (2)如图 2,若,AC 和 BD 相交于点 P,求证:OP平分. (3)如图 3 所示,则AC 与 BD 的数量关系为________________,试用表示直线 AC 和 BD 所形成的夹角,则夹角为______________.(不写证明) ααCBAEFD90 60 BPC图1图2图3ABCDOPABCDOPODCBA题型一 “手拉手”模型 “帽子”模型常见辅助线做法: ⑴作平行线构造全等 ⑵作垂直构造全等 已知AB=AC,BE=CF,EF 交BC 于D,则DE=DF. 已知AB=AC,BE=CF,EF 交BC 于D, EH⊥BC 于H,则DH= 12 BC 【例2】(2013 年武汉二中,2015 年 81 中月考)如图 1,已知A(0,a ), B(b ,0),且 a 、b 满足224208aabb. (1) 求 A、B 两点的坐标; (2) 如图 2,连接 AB,若(0, 6)D,DE⊥AB 于点 E,B、C 关于y轴对称,M 是线段 DE 上的一点,且 DM=AB, 连接 AM,试判断线段 AC 与 AM 之间的位置和数量关系, 并证明你的结论; (3) 如图 3,在(2)的条件下,若 N 是线段 DM 上的一个动点,P 是 MA 延长线上的一点,且 DN=AP,连接 PN 交y轴于点 Q,过点 N 作 NH⊥ y轴于点 H,当 N 点在线段 DM 上运动时,△MQH 的面积是否为定值?若是,请求出这个值;若不是,请说明理由. DFEABCCBAEFDH题型二 帽子模型 OAByxEDxyBAOCMOxyMADNPQH 3 / 8 夹半角模型的证明核心是“图形的旋转”,以旋转造全等,已知AB=AC,∠BAC=2∠DAF,则构造△AEB≌△AFC,进而可以证明△ADE≌△ADF 【例3】(2015 年·二十五中期中)如图,已知A(a,0)、B(0,b),且 a、b 满足(a-2)2+|2b-4|=0 (1) 如图1,求△AOB 的面积 (2) 如图2,点 C 在线段 AB 上(不与 A、B 重合)移动,AB⊥BD,且∠COD=45° ,猜想线段 AC、BD、CD 之间的数量关系并证明你的结论. (3) 如图3,若 P 为 x 轴上异于原点 O 和点 A 的一个动点,连接 PB,将线段 PB 绕点 P 顺时针旋转90°至 PE,直线 AE 交 y 轴于点 Q,当 P 点在 x...