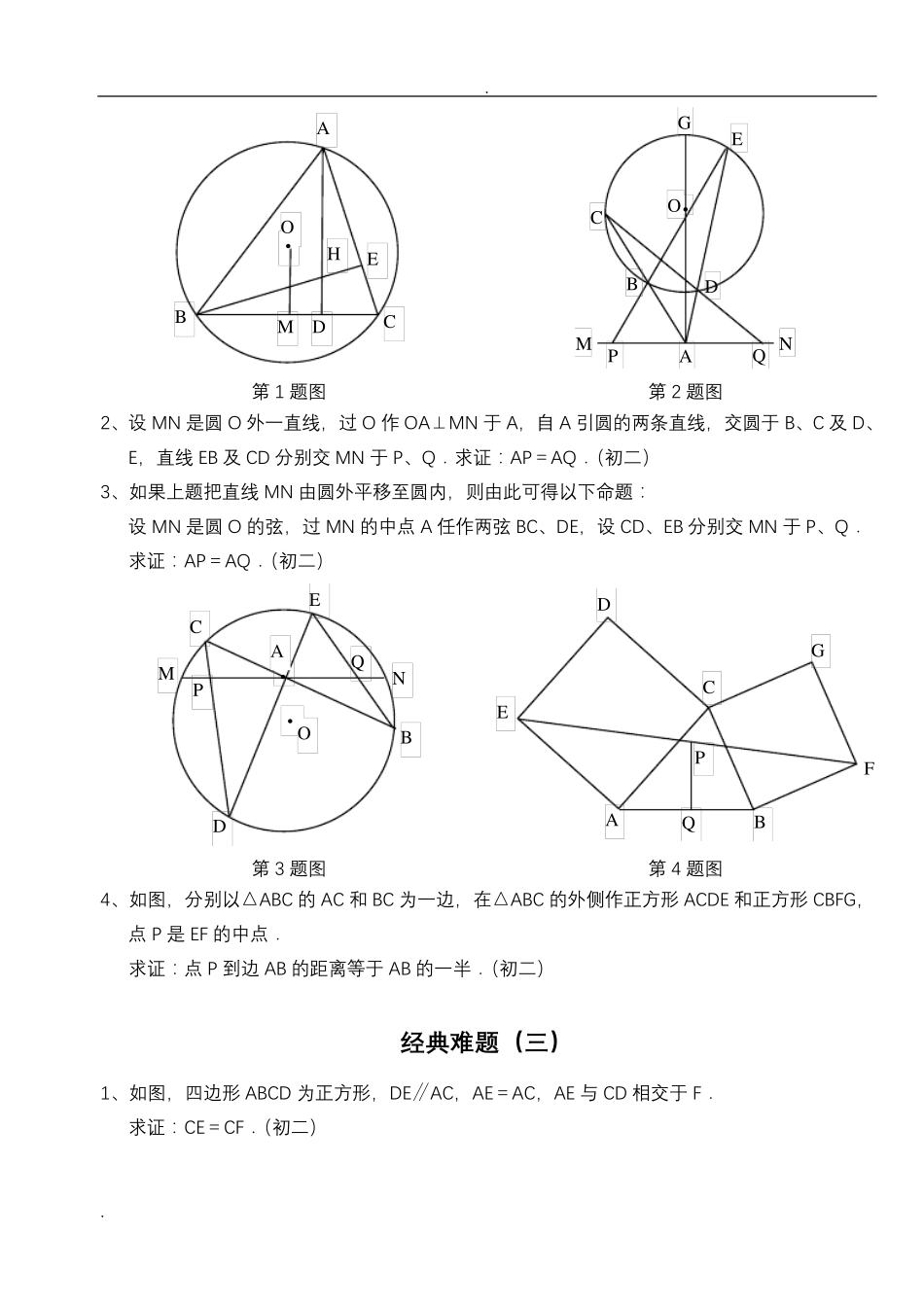
. . 经 典 难 题 ( 一 ) 1、 已 知 : 如 图 , O 是 半 圆 的 圆 心 , C、 E 是 圆 上 的 两 点 , CD⊥ AB, EF⊥ AB, EG⊥ CO. 求 证 : CD= GF.( 初 二 ) 第 1 题 图 第 2 题 图 2、 已 知 : 如 图 , P 是 正 方 形 ABCD 内 点 , ∠ PAD= ∠ PDA= 150. 求 证 : △ PBC 是 正 三 角 形 .( 初 二 ) 3、 如 图 , 已 知 四 边 形 ABCD、 A1B1C1D1都 是 正 方 形 , A2、 B2、 C2、 D2分 别 是 AA1、 BB1、 CC1、 DD1的 中 点 . 求 证 : 四 边 形 A2B2C2D2是 正 方 形 .( 初 二 ) 第 3 题 图 第 4 题 图 4、 已 知 : 如 图 , 在 四 边 形 ABCD 中 , AD= BC, M、 N 分 别 是 AB、 CD 的 中 点 , AD、 BC 的 延 长线 交 MN 于 E、 F. 求 证 : ∠ DEN= ∠ F. 经 典 难 题 ( 二 ) 1、 已 知 : △ ABC 中 , H 为 垂 心 ( 各 边 高 线 的 交 点 ), O 为 外 心 , 且 OM⊥ BC 于 M. ( 1) 求 证 : AH= 2OM; ( 2) 若 ∠ BAC= 600, 求 证 : AH= AO.( 初 二 ) A N F E C D M B D2 C2 B2 A2 D1 C1 B1 C B D A A1 A P C D B A F G C E B O D . . 第 1 题 图 第 2 题 图 2、 设 MN 是 圆 O 外 一 直 线 , 过 O 作 OA⊥ MN 于 A, 自 A 引 圆 的 两 条 直 线 , 交 圆 于 B、 C 及 D、E, 直 线 EB 及 CD 分 别 交 MN 于 P、 Q. 求 证 : AP= AQ.( 初 二 ) 3、 如 果 上 题 把 直 线 MN 由 圆 外 平 移 至 圆 内 , 则 由 此 可 得 以 下 命 题 : 设 MN 是 圆 O 的 弦 , 过 MN 的 中 点 A 任 作 两 弦 BC、 DE, 设 CD、 EB 分 别 交 MN 于 P、 Q. 求 证 : AP= AQ.( 初 二 ) 第 3 题 图 第 4 题 图 4、 如 图 , 分 别 以 △ ABC 的 AC 和 BC 为 一 边 , 在 △ ABC 的 外 侧 作 正 方 形 ACDE 和 正 方 形 CBFG,点 P 是 EF 的 中 点 . 求 证 : 点 P 到 边 AB 的 距 离 等 于 AB ...