平面和平面垂直的性质课件VIP免费

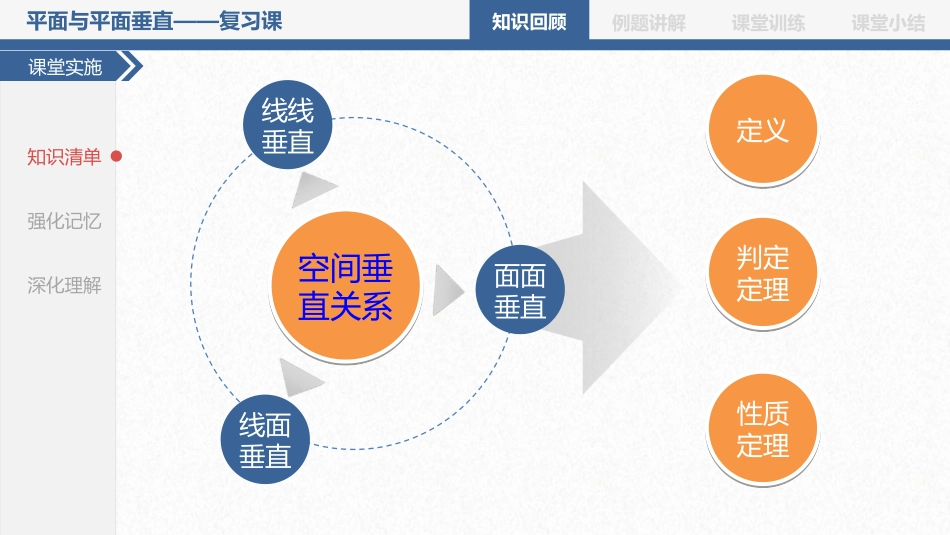
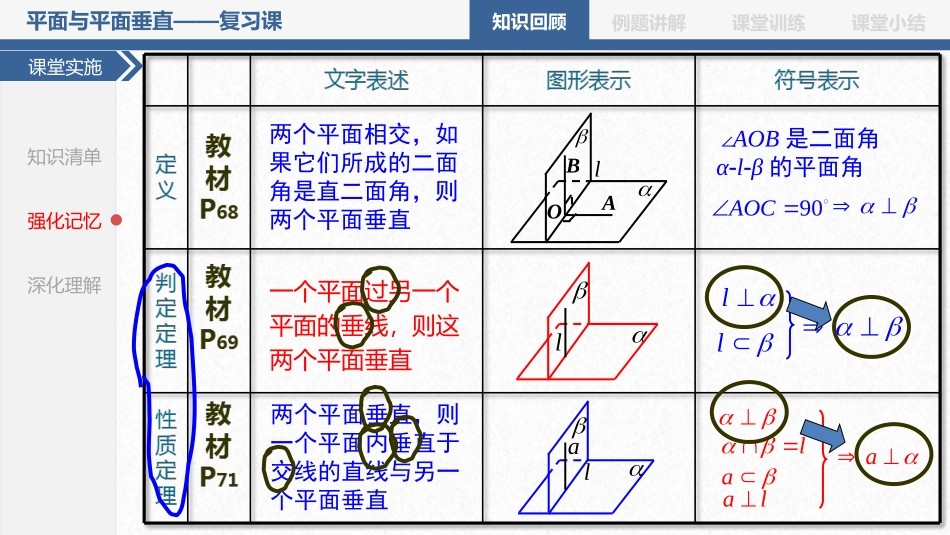
HainanoverseasChinesemiddleschool例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课知识回顾课堂实施知识清单强化记忆深化理解线线垂直线面垂直空间垂直关系空间垂直关系定义定义面面垂直判定定理判定定理性质定理性质定理例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课知识回顾laalalal90AOC一个平面过另一个平面的垂线，则这两个平面垂直两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直两个平面相交，如果它们所成的二面角是直二面角，则两个平面垂直lOABll课堂实施知识清单强化记忆深化理解∠AOB是二面角α-l-β的平面角例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课知识回顾CADB课堂实施知识清单强化记忆深化理解“三节棍”模型“三节棍”模型教材69页探究：如图，已知AB⊥平面BCD，BC⊥CD，你能发现哪些平面互相垂直，为什么？在一个平面内找另一个平面的垂线例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题规范解答解题反思各抒己见分析提炼典题ABCDOP（2）证明：平面POC⊥平面ABCD.（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．分析问题（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．（1）你能发现哪些平面一定相互垂直？变式提升分析条件例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题ABCD是直角梯形AB⊥ADABCD∥AB=2CD侧面PAB垂直于底面ABCDPA＝PBO是AB的中点分析条件典题规范解答ABCDOP（2）证明：平面POC⊥平面ABCD.直角梯形两面垂直等腰三角形梯形的一些平面性质面面垂直的性质定理三线合一ABCDO11面面垂直线面垂直22PBAO33例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．分析提炼各抒己见（1）你能发现哪些平面一定相互垂直？解题反思变式提升例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题典题各抒己见分析提炼规范解答ABCDOP（2）证明：平面POC⊥平面ABCD.（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．ABCDO面面垂直线面垂直PBAO分析条件：面面垂直线面垂直线在面内面面垂直垂直交线分析问题：解题反思变式提升例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题典题各抒己见分析提炼规范解答ABCDOP（2）证明：平面POC⊥平面ABCD.（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，；且PA＝PB，O是AB的中点．侧面PAB垂直于底面ABCD，AB=2CD变式：若侧面PAB不垂直于底面ABCD，问题（2）的结论还成立吗？.ABCDOP解题反思变式提升例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题典题各抒己见分析提炼规范解答反思1认真读题，深入思考挖掘题目的隐含条件2借用熟悉的模型和模具认清几何体的特征ABCDOP4从要证（要求）的结论出发“执果索因”3关注几何体中平面图形的性质立体几何问题平面化思考5证明面面垂直要在一个平面内找另一个平面的垂线给两个平面垂直要在一个平面内找垂直于交线的直线定理的通俗化记忆解题反思变式提升例题讲解课堂训练课堂小结知识回顾平面与平面垂直——复习课典型例题5对规范解答解题反思各抒己见分析提炼典题ABCDOP（1）你能发现哪些平面一定相互垂直？例：如图四棱锥P-ABCD的底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2CD；侧面PAB垂直于底面ABCD，且PA＝PB，O是AB的中点．（1）你能发现哪些平面一定相...