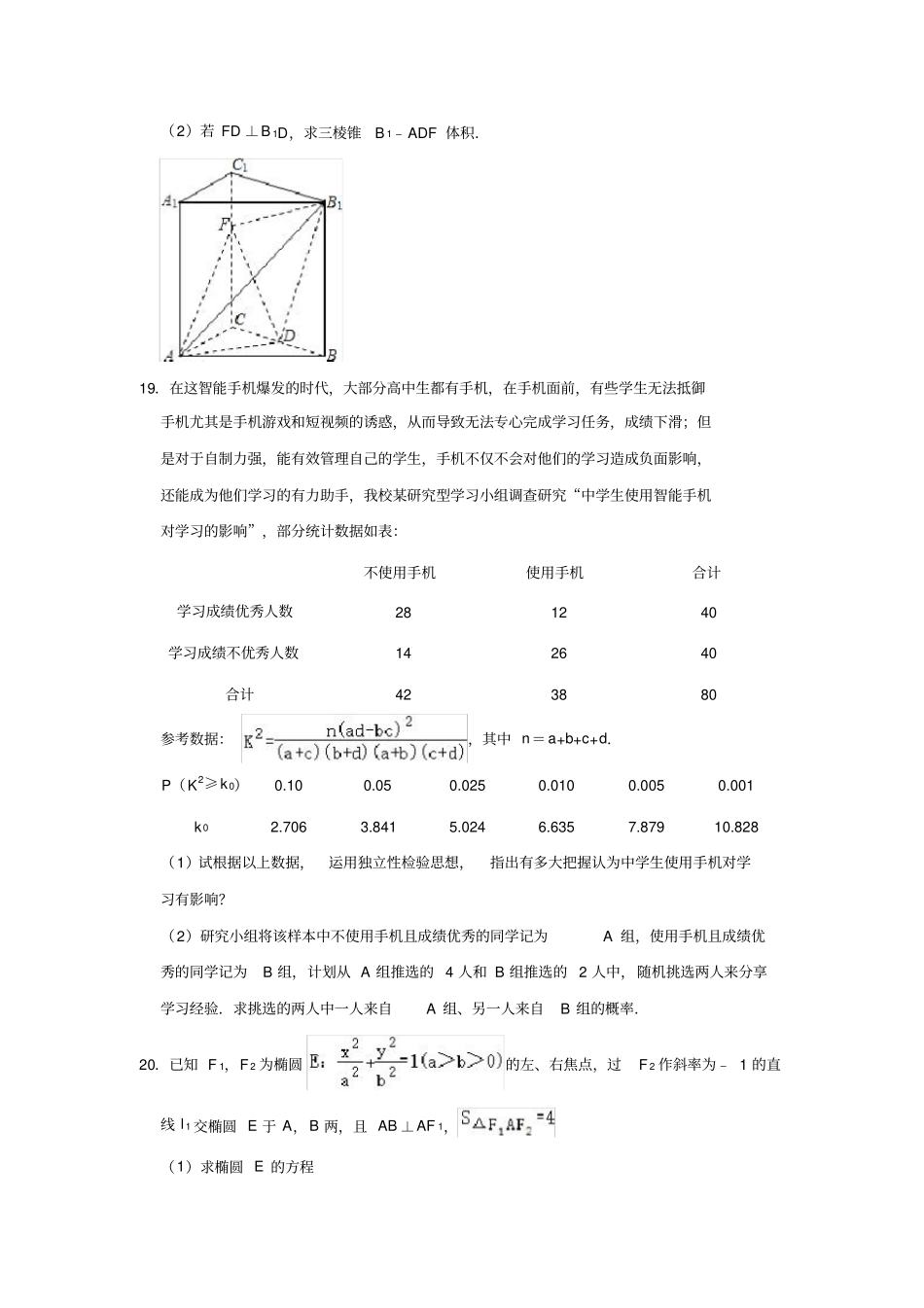
2020 年高考数学( 4 月份)模拟试卷(文科)一、选择题1.已知集合A={1,0,﹣ 1},B={y|y=2x﹣1,x∈A},则 A∩B=()A.{1,0,﹣ 1}B.{1,﹣ 1}C.{0}D.?2.已知 i 为虚数单位,则复数z=2i﹣的虚部是()A.3iB.iC.3D.13.已知数列 {an} 为等差数列,前n 项和为 Sn,且 a5=5,则 S9=()A.25B.90C.50D.454.已知直线l,m,平面 α、β、 γ,给出下列命题:① l∥ α,l∥β,α∩ β=m,则 l∥m;②α ∥β,β∥ γ,m⊥α,则 m⊥ γ;③α ⊥γ,β⊥γ,则 α⊥ β;④ l⊥ m, l⊥α,m⊥β,则 α⊥β.其中正确的命题有()A.1 个B.2 个C.3 个D.4 个5.若 ||=,||=2 且(﹣)⊥,则与的夹角是()A.B.C.D.6.计算 sin133° cos197° +cos47° cos73° 的结果为()A.B.C.D.﹣7.已知抛物线y2=4x 的焦点到双曲线(a>0)的一条渐近线的距离为,则该双曲线的方程为()A.x2﹣y2=1B.﹣y2=1C.﹣y2=1D.﹣y2=18.若 x,y 满足约束条件,则 z=4x+3y 的最小值为()A.9B.6.5C.4D.39.定义在R 上的奇函数f(x)= a? 2x﹣2﹣x﹣4sinx 的一个零点所在区间为()A.(﹣ a,0)B.( 0, a)C.( a,3)D.( 3,a+3)10.若直线 l :4x﹣ay+1=0 与圆 C:(x+2)2+( y﹣2)2=4 相切,则实数a 的值为()A.B.C.或 1D.或 111.已知四棱锥的各个顶点都在同一个球的球面上,且侧棱长都相等,高为4,底面是边长为 3的正方形,则该球的表面积为()A.B.C.36πD.34π12.关于 x 的方程 kx=sinx(k∈(0,1))在(﹣ 3π,3π)内有且仅有5 个根,设最大的根是 α,则 α 与 tan α 的大小关系是()A.α> tanαB.α< tanαC.α=tan αD.以上都不对二、填空题(共4 小题)13.如图,在△ ABC 中,∠ B=45° , D 是 BC 边上的一点, AD=5, AC=7,DC=3,则AB 的长为.14.已知正实数a,b 满足= 3,则( a+1)( b+2)的最小值是.15.设 m>0,点 A(4,m)为抛物线y2=2px(p>0)上一点, F 为焦点,以A 为圆心 |AF |为半径的圆C 被 y 轴截得的弦长为6,则圆 C 的标准方程为.16.定义在R 上的函数f(x)满足 f'(x)﹣ f( x)< 2ex(e 为自然对数的底数),其中f'(x)为 f( x)的导函数,若f(2)= 4e2,则>xex 的解集为.三、解答题(共6 ...