北大版高等数学第三章积分的计算及应用答案习题3.5

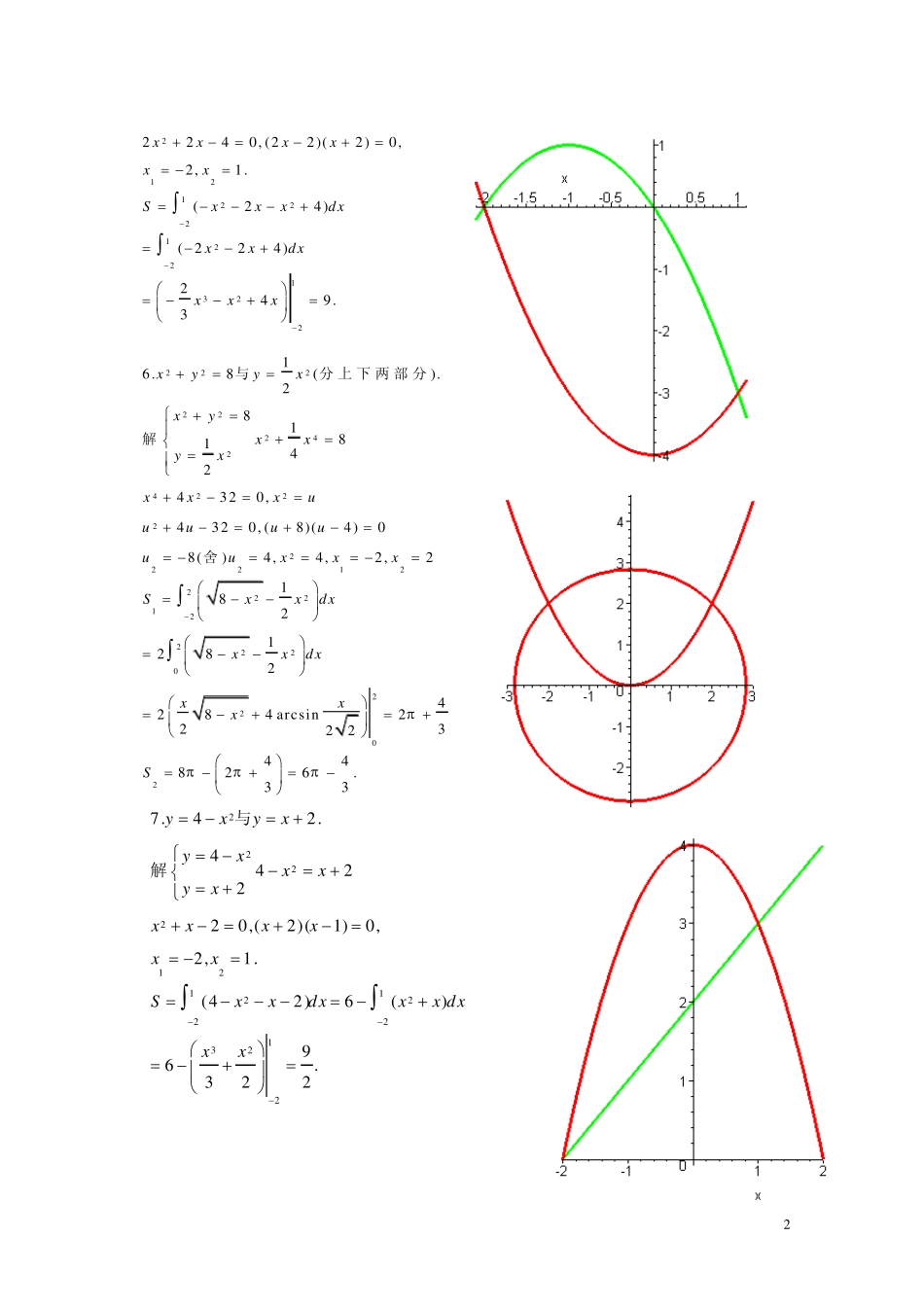
1 习题3 . 213212002.,1.43(2).22xyx yyySyy dyy与解 222232132313.211.21(1)21,140,0,1;4,3.11(1)23116 .2263yxxyyxxxxyxxxyxySyydxyyy 与解 2222225.42 .442 ,2yxyxxyxxxxyxx   与解 2224221123 / 2200:1..,,(1)(1)0,0,1.211().333yxxyyxxxxyxxxxxxSxxdxxx求下 列 曲 线 所 围 成 的 的 图 形 的 面 积与求交 点解:2022202242400/ 224202(sin )4.0 02(a>0)(1cos )(1cos )(sin )(1cos )4sin8sin2316sin164 223.xa ttytyatSat da ttatdttadtauduauduaa与 2 212122212213222240, (22)(2)0,2,1.(24)(224)249.3xxxxxxSxxxdxxxdxxxx 2222224242222221222212222022016.8().28181424320,4320, (8)(4)08()4,4,2,218212824284 arcs in22322xyyxxyxxyxxxxuuuuuuuxxxSxxdxxxdxxxxS  与分上 下 两 部 分舍解244826.3322221211222213227.42.442220,(2)(1)0,2,1.(42)6()96.322yxyxyxxxyxxxxxxxSxxdxxx dxxx 与解 3 22/ 422/ 42008.cos 2(0).1cos 22sin 2|.2raaadaa 其求双纽线所围图形的面积1解S = 42 2 / 32 / 32 / 333/ 2226200/ 23720/ 237203:9.(0).cos, 02.sin22sin3 cossin6sincos6sin(1sin)6 4 2832617 5 391axyaaxattyatVy dxatattdtattdtatt dta  求下 列 曲 线围成 的平 面图形绕 轴 旋 转所成 旋 转 体 的体 积解3.05aln 3ln 32200ln 32010.1,ln 3,.(1)(21)12ln 3.2xxxxxxyexyeVedxeedxeex231 / 32 / 31...