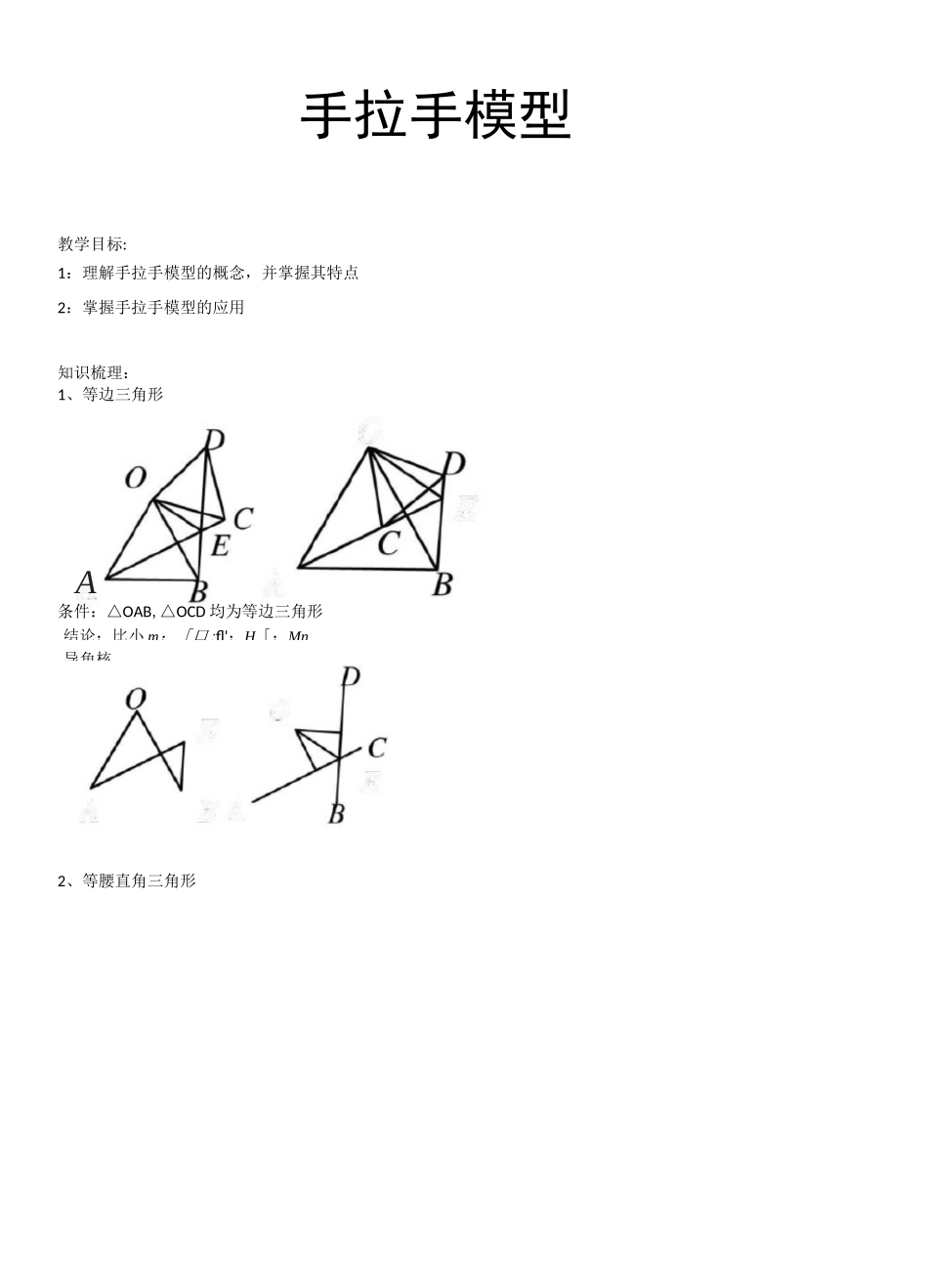
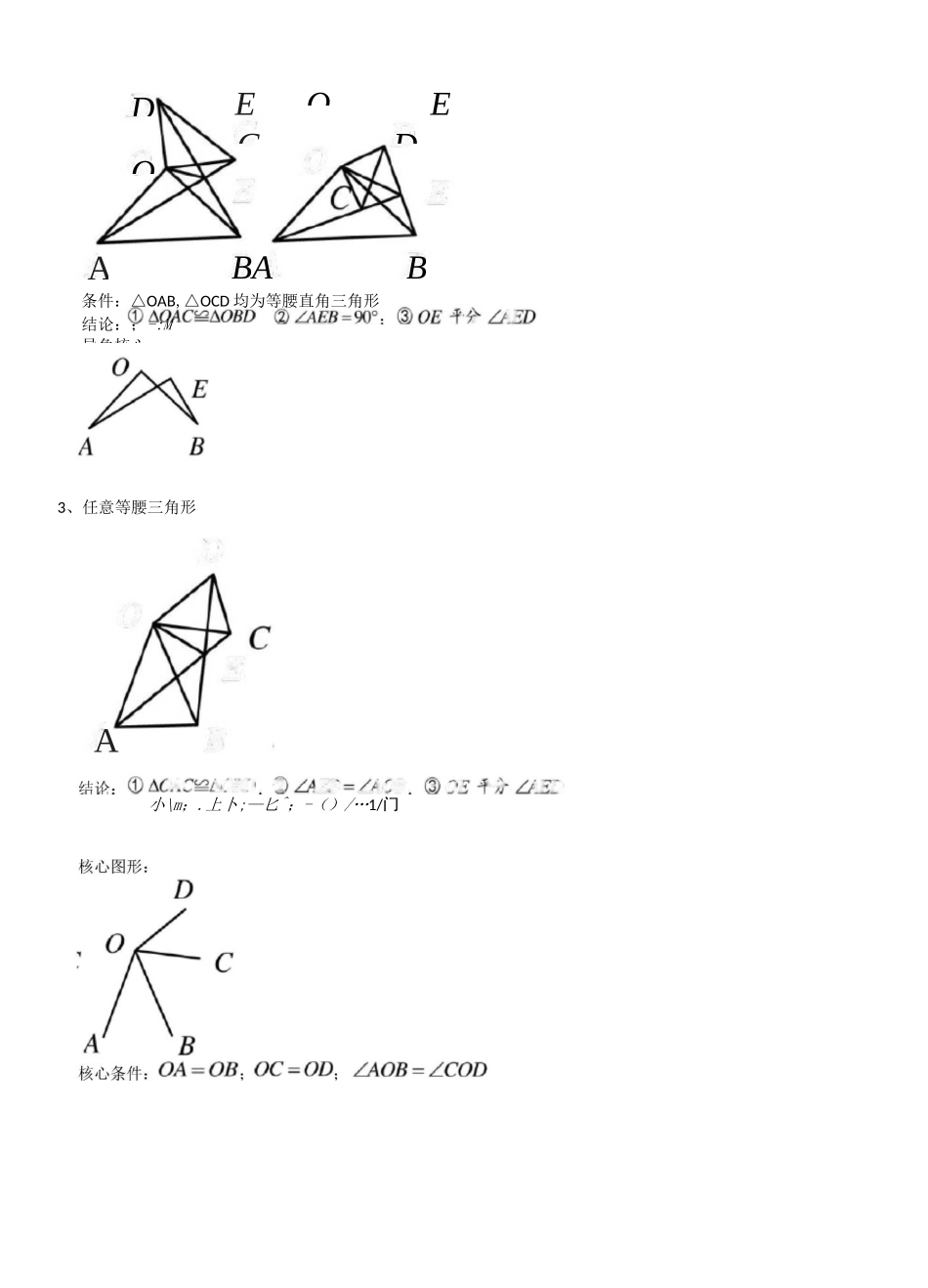
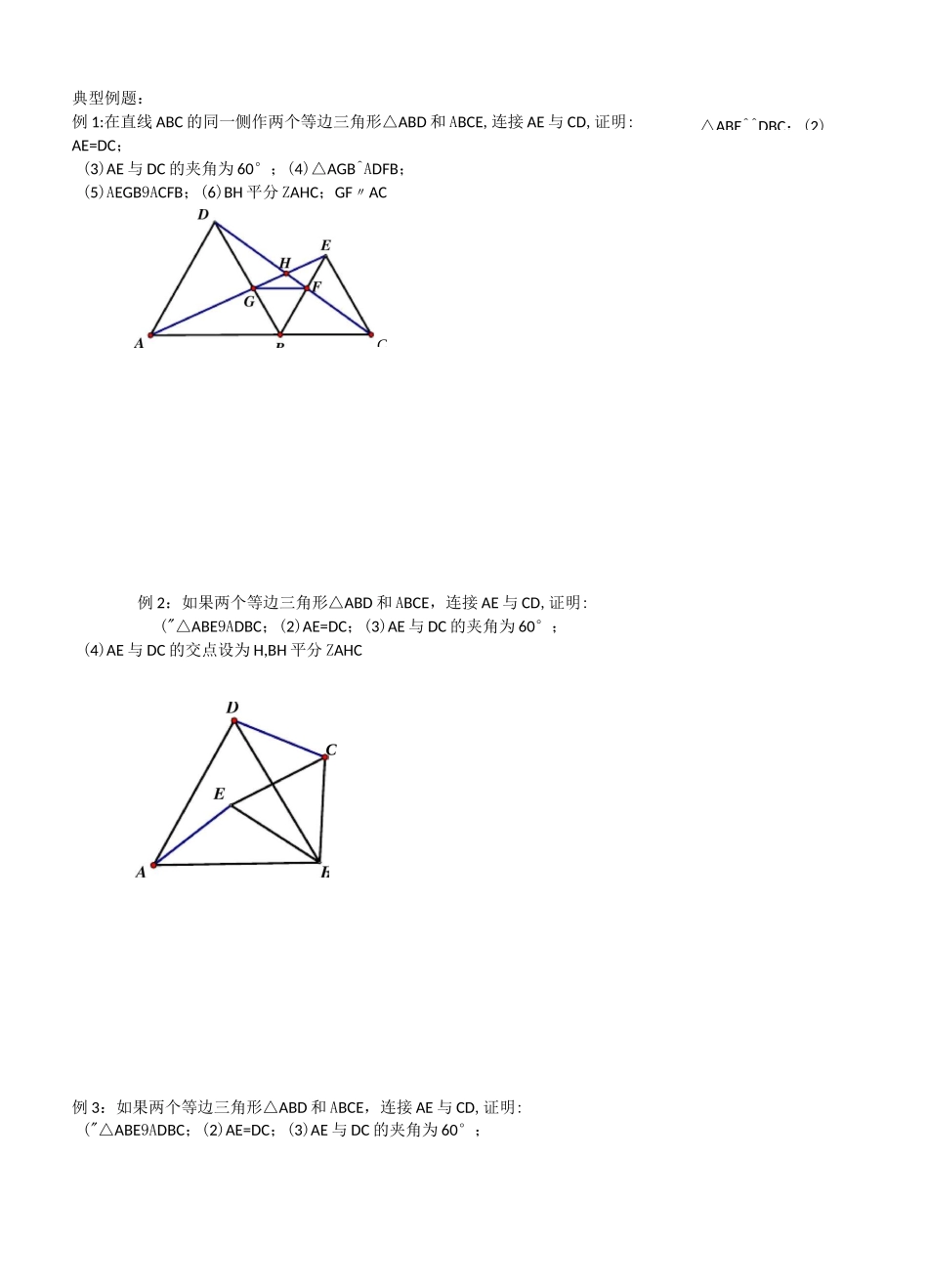
结论:比小 m;「口;fl';H「:Mn0EE导角核手拉手模型教学目标:1:理解手拉手模型的概念,并掌握其特点2:掌握手拉手模型的应用知识梳理:1、等边三角形A条件:△OAB,△OCD 均为等边三角形2、等腰直角三角形3、任意等腰三角形小\m;.上卜;—匕^;-()/…1/门DCDOOEEBABA条件:△OAB,△OCD 均为等腰直角三角形结论:;-:M导角核心:AB△ABE^^DBC;(2)典型例题:例 1:在直线 ABC 的同一侧作两个等边三角形△ABD 和 ABCE,连接 AE 与 CD,证明:AE=DC;(3)AE 与 DC 的夹角为 60°;(4)△AGB^ADFB;(5)AEGB9ACFB;(6)BH 平分 ZAHC;GF〃AC例 2:如果两个等边三角形△ABD 和 ABCE,连接 AE 与 CD,证明:("△ABE9ADBC;(2)AE=DC;(3)AE 与 DC 的夹角为 60°;(4)AE 与 DC 的交点设为 H,BH 平分 ZAHC例 3:如果两个等边三角形△ABD 和 ABCE,连接 AE 与 CD,证明:("△ABE9ADBC;(2)AE=DC;(3)AE 与 DC 的夹角为 60°;CC(4)AE 与 DC 的交点设为 H,BH 平分 ZAHC例 4:如图,两个正方形 ABCD 和 DEFG,连接 AG 与 CE,二者相交于 H问:(1)△ADG^^CDE 是否成立?(2)AG 是否与 CE 相等?(3)AG 与 CE 之间的夹角为多少度?(4)HD 是否平分 ZAHE?例 5:如图两个等腰直角三角形 ADC 与 EDG,连接 AG,CE,二者相交于 H.问(DAADG^ACDE 是否成立?(2)AG 是否与 CE 相等?例 6:两个等腰三角形 ABD 与 BCE,其中 AB=BD,CB=EB,ZABD=ZCBE,连接 AE 与 CD.问否成立?(2)AE 是否与 CD 相等?(3)AE 与 CD 之间的夹角为多少度?(4)HB 是否平分 ZAHC?(1)△ABE^^DBC 是(3)AG 与 CE 之间的夹角为多少度?(4)HD 是否平分 ZAHE?例 7:如图,分别以厶 ABC 的边 AB、AC 同时向外作等腰直角三角形,其中 AB=AE,AC=AD,ZBAE=ZCAD=90°,点 G 为 BC 中点,点 F 为 BE 中点,点 H 为 CD 中点。探索 GF 与 GH 的位置及数量关系并说明理由。例 8:如图 1,已知 ZDAC=90°,△ABC 是等边三角形,点 P 为射线 AD 任意一点(P 与 A 不重合),连结 CP,将线段 CP 绕点 C 顺时针旋转 60°得到线段 CQ,连结 QB 并延长交直线 AD 于点 E.(1)如图 1,猜想 ZQEP=°;上 C8團 1(2)如图 2,3,若当 ZDAC 是锐角或钝角时,其它条件不变,猜想 ZQEP 的度数,选取一种情况加以证明;團 2 團 M(3)如图 3,若 ZDAC=135°,ZACP=15°,且...