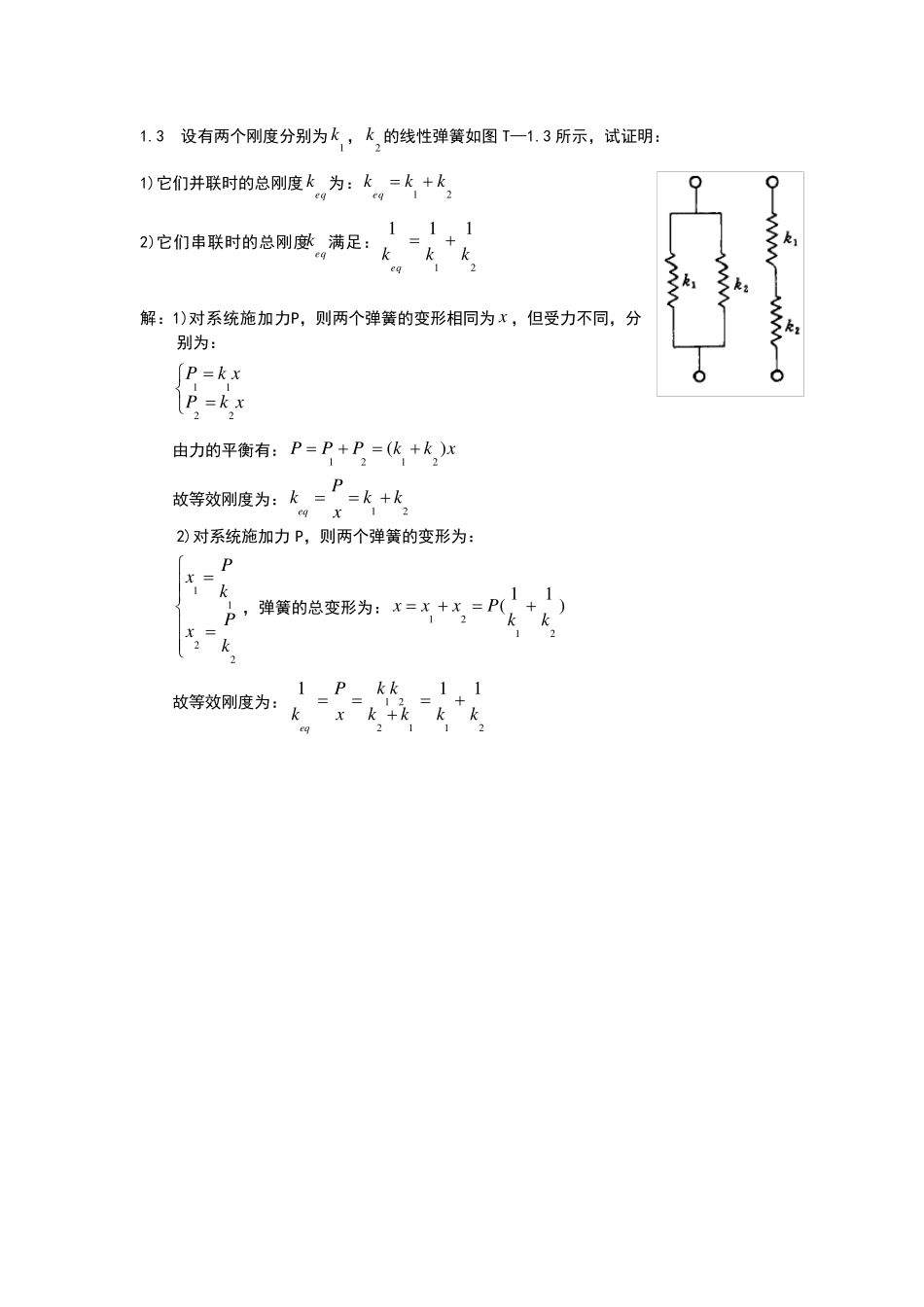
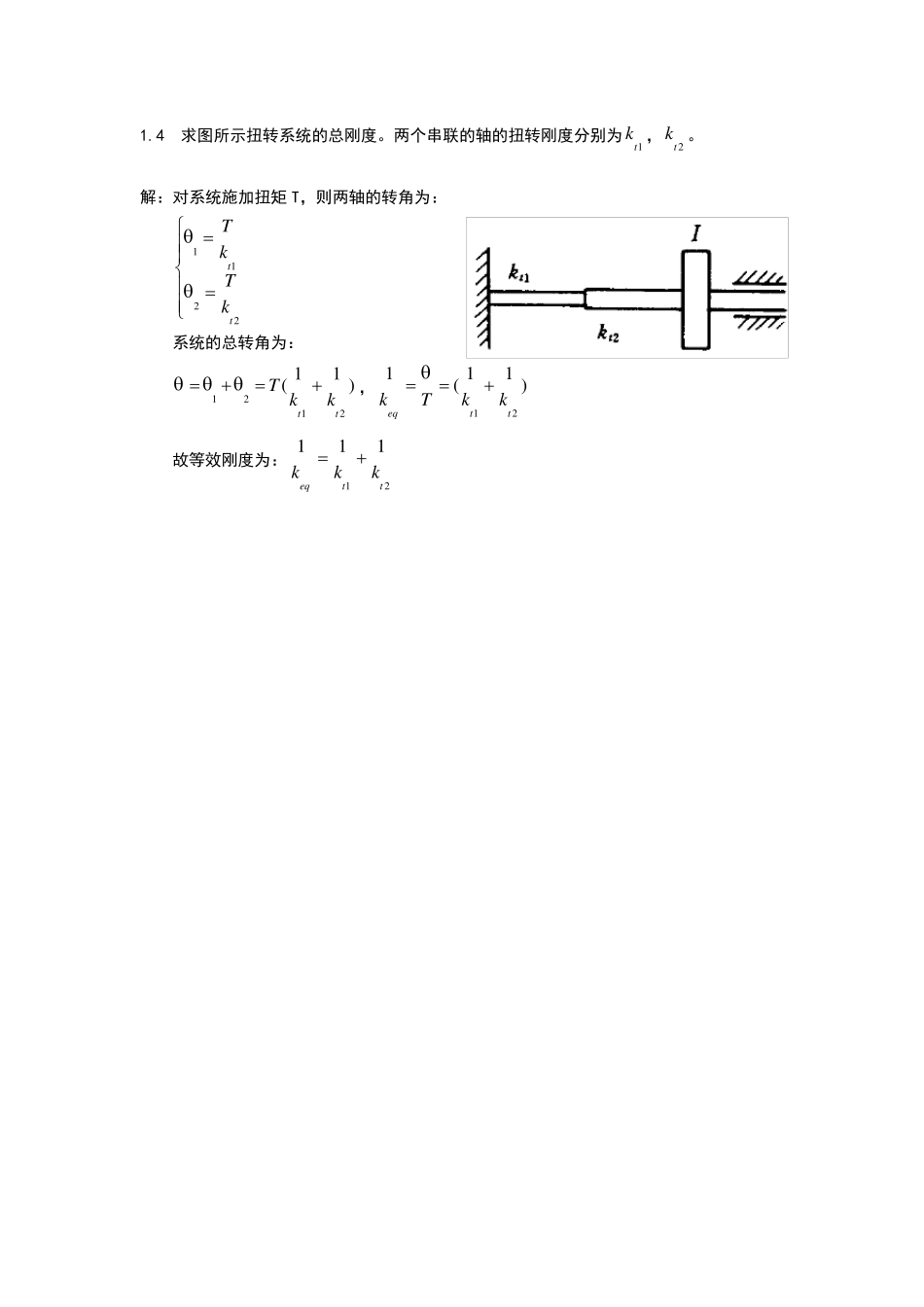
1.1 试举出振动设计、系统识别和环境预测的实例。 1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度? 1.3 设有两个刚度分别为1k ,2k 的线性弹簧如图T—1.3 所示,试证明: 1)它们并联时的总刚度eqk为:21kkkeq 2)它们串联时的总刚度eqk满足:21111kkkeq 解:1)对系统施加力P,则两个弹簧的变形相同为x ,但受力不同,分别为: 1122Pk xPk x 由力的平衡有:1212()PPPkkx 故等效刚度为:12eqPkkkx 2)对系统施加力 P,则两个弹簧的变形为: 1122PxkPxk,弹簧的总变形为:121211()xxxP kk 故等效刚度为:122112111eqk kPkxkkkk 1.4 求图所示扭转系统的总刚度。两个串联的轴的扭转刚度分别为1tk ,2tk。 解:对系统施加扭矩 T,则两轴的转角为: 1122ttTkTk 系统的总转角为: 121211()ttT kk,12111()eqttkTkk 故等效刚度为:12111eqttkkk 1.5 两只减振器的粘性阻尼系数分别为1c ,2c ,试计算总粘性阻尼系数eqc 1)在两只减振器并联时, 2)在两只减振器串联时。 解:1)对系统施加力P,则两个减振器的速度同为x ,受力分别为: 1122Pc xPc x 由力的平衡有:1212()PPPccx 故等效刚度为:12eqPcccx 2)对系统施加力 P,则两个减振器的速度为: 1122PxcPxc,系统的总速度为:121211()xxxP cc 故等效刚度为:1211eqPcxcc 1.6 一简谐运动,振幅为0.5cm,周期为0.15s,求最大速度和加速度。 解:简谐运动的22(/ )0.15nrad sT ,振幅为35 10 m; 即:3332225 10cos()( )0.15225 10sin()(/ )0.150.15225 10() cos()(/)0.150.15xt mxtt m sxtt m s 所以:3max322max25 10(/ )0.1525 10() (/)0.15xm sxm s 1.7 一加速度计指示出结构振动频率为82Hz,并具有最大加速度50g,求振动的振幅。 解:由 2maxnxA 可知: 2maxmax2222250 9.8/9.8(2)(225) 1/50nxxm sAmfs 1.8 证明:两个同频率...