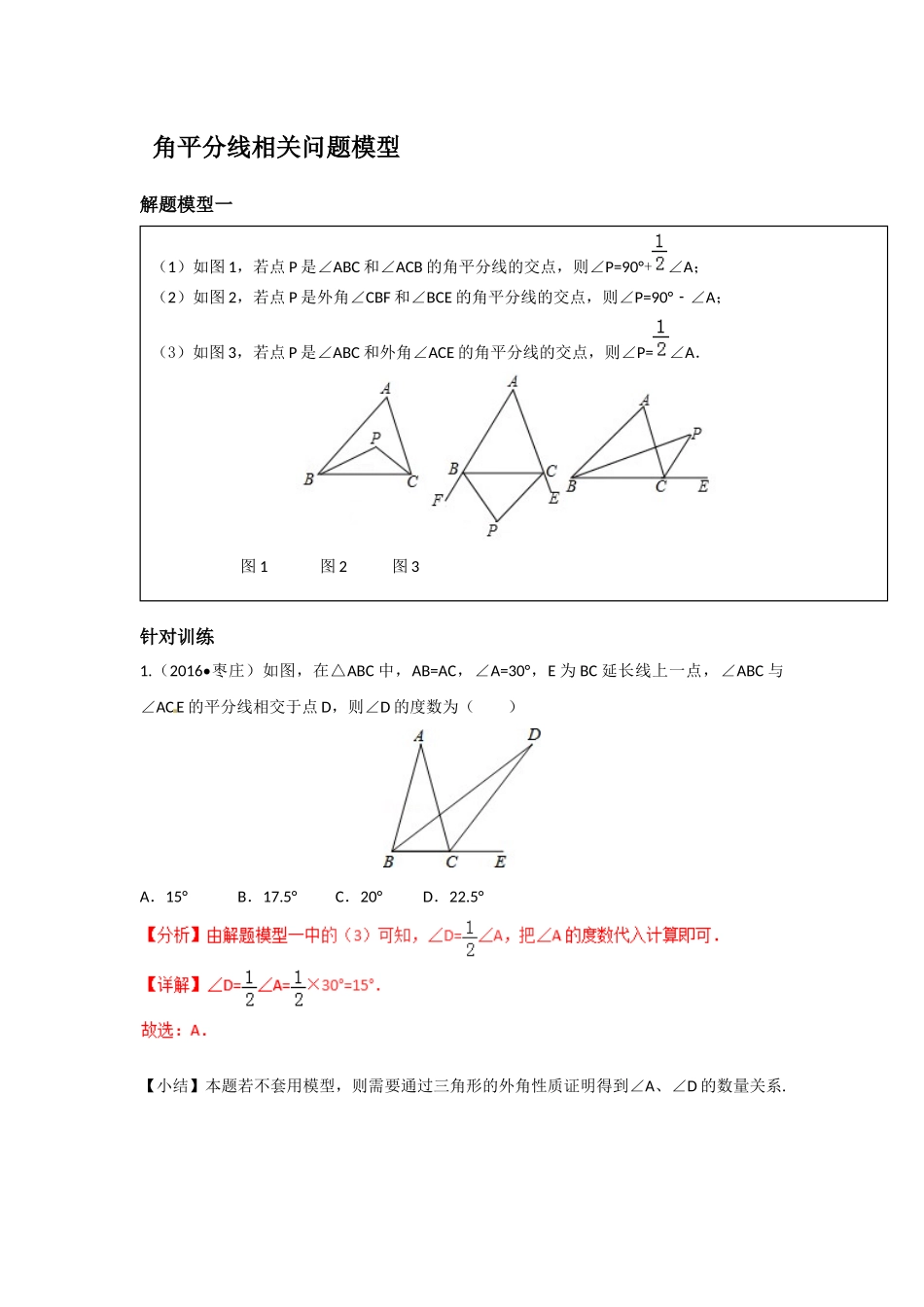
角平分线相关问题模型解题模型一针对训练1.(2016•枣庄)如图,在△ABC 中,AB=AC,∠A=30°,E 为 BC 延长线上一点,∠ABC 与∠ACE 的平分线相交于点 D,则∠D 的度数为( )A.15° B.17.5° C.20° D.22.5°【小结】本题若不套用模型,则需要通过三角形的外角性质证明得到∠A、∠D 的数量关系.(1)如图 1,若点 P 是∠ABC 和∠ACB 的角平分线的交点,则∠P=90°+∠A;(2)如图 2,若点 P 是外角∠CBF 和∠BCE 的角平分线的交点,则∠P=90°﹣∠A;(3)如图 3,若点 P 是∠ABC 和外角∠ACE 的角平分线的交点,则∠P=∠A. 图 1 图 2 图 32.(2018•巴中)如图,在△ABC 中,BO、CO 分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A= .【分析】由解题模型一中的(1)可知,∠BOC=90°+∠A,把∠BOC=110°代入计算可得到∠A 的度数.【详解】∵∠BOC=90°+∠A,∠BOC=110°,∴90°+∠A=110°.∴∠A=40°.【小结】本题若不套用模型,需要利用三角形的内角和定理、角平分线的定义得到 ∠BOC、∠A 的数量关系.3.(2018•济南历城区模拟)如图,BA1 和 CA1 分别是△ABC 的内角平分线和外角平分线,BA2是∠A1BD 的角平分线,CA2是∠A1CD 的角平分线,BA3是∠A2BD 的角平分线,CA3是∠A2CD 的角平分线,若∠A1=α,则∠A2018= .【详解】∵A1B 是∠ABC 的平分线,A1C 是∠ACD 的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键。