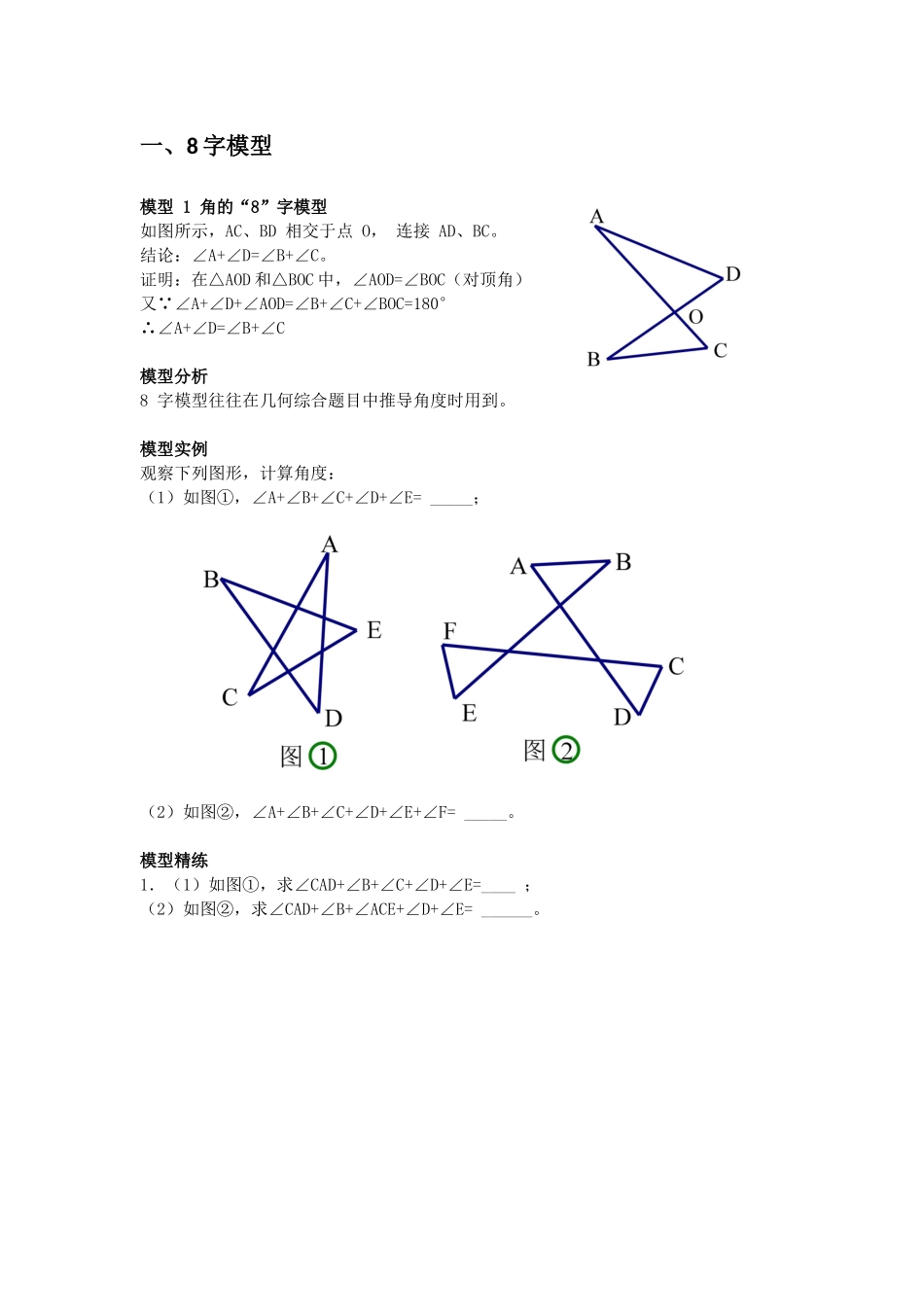
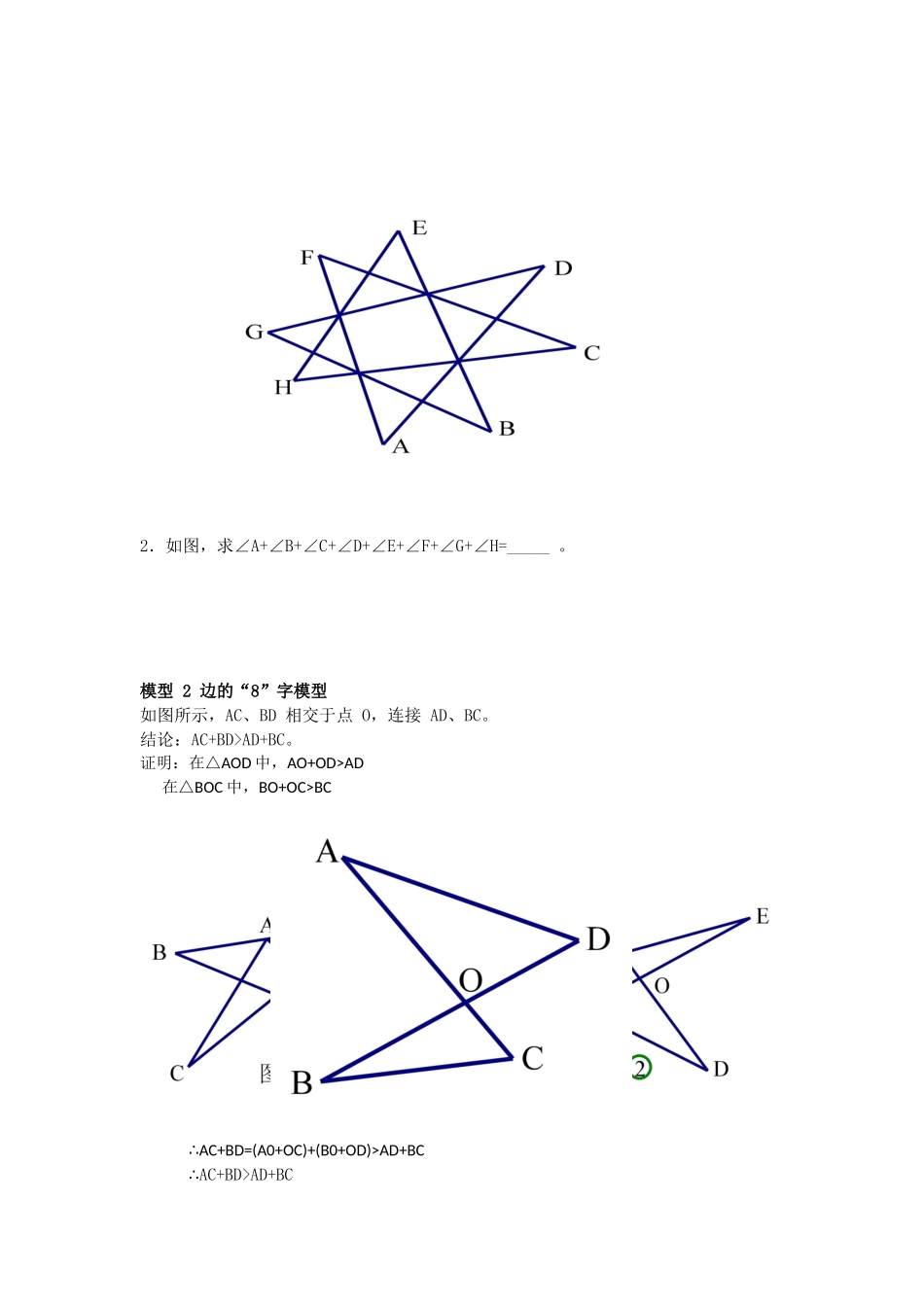
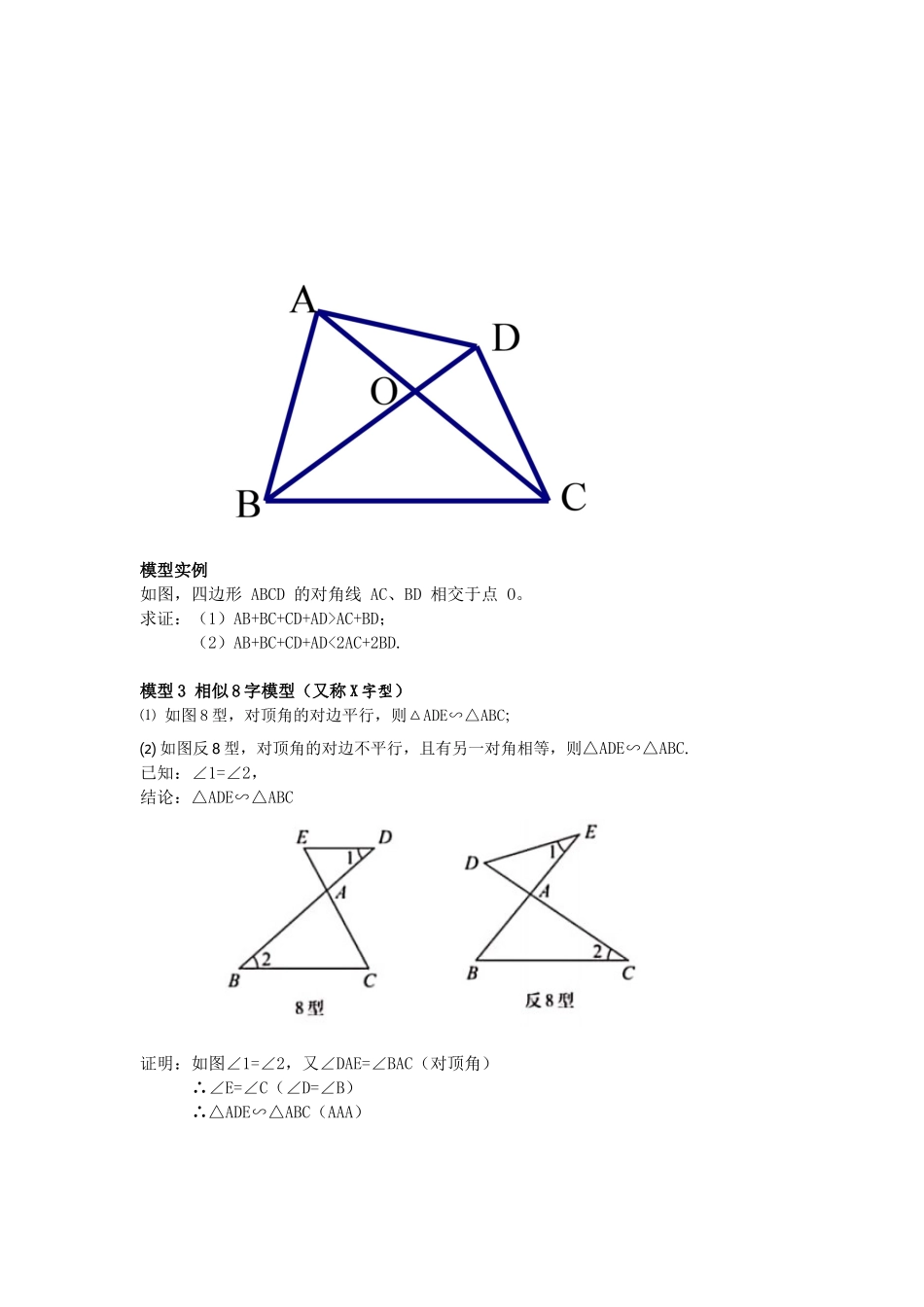
一、8 字模型 模型 1 角的“8”字模型 如图所示,AC、BD 相交于点 O, 连接 AD、BC。 结论:∠A+∠D=∠B+∠C。 证明:在△AOD 和△BOC 中,∠AOD=∠BOC(对顶角)又∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°∴∠A+∠D=∠B+∠C模型分析8 字模型往往在几何综合题目中推导角度时用到。 模型实例观察下列图形,计算角度: (1)如图①,∠A+∠B+∠C+∠D+∠E= _____; (2)如图②,∠A+∠B+∠C+∠D+∠E+∠F= _____。 模型精练 1.(1)如图①,求∠CAD+∠B+∠C+∠D+∠E=____ ; (2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E= ______。 2.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=_____ 。模型 2 边的“8”字模型 如图所示,AC、BD 相交于点 O,连接 AD、BC。 结论:AC+BD>AD+BC。 证明:在△AOD 中,AO+OD>AD 在△BOC 中,BO+OC>BCAC+BD=(A0+OC)+(B0+OD)>AD+BC∴∴AC+BD>AD+BC模型实例如图,四边形 ABCD 的对角线 AC、BD 相交于点 O。 求证:(1)AB+BC+CD+AD>AC+BD; (2)AB+BC+CD+AD<2AC+2BD. 模型 3 相似 8 字模型(又称 X 字型)⑴ 如图 8 型,对顶角的对边平行,则△ADE∽△ABC; ⑵ 如图反 8 型,对顶角的对边不平行,且有另一对角相等,则△ADE∽△ABC.已知:∠1=∠2,结论:△ADE∽△ABC证明:如图∠1=∠2,又∠DAE=∠BAC(对顶角) ∴∠E=∠C(∠D=∠B) ∴△ADE∽△ABC(AAA)模型分析在相似三角形的判定中,我们常通过作平行线,从而得到 8 字形相似(有时得到 A 字形相似,后面会讲到),在做题时,我们也常常关注题目中由平行线产生的相似三角形。以下题目由沈阳数学高老师提供模型例题:如图,△ABC 是等边三角形,CE 是外角平分线,点 D 在 AC 上,连接 BD 并延长与 CE 交于点 E.⑴ 求证:△ABD∽△CED;⑵ 若 AB=6,AD=2CD,求 BE 的长.练习:1. 如图 7,点 P 是□ABCD 边 AB 上的一点,射线 CP 交 DA 的延长线于点 E,则图中相似的三角形有( ) A. 0 对 B. 1 对 C. 2 对 D. 3 对2.如图 8,正方形 ABCD 的对角线 AC 与 BD 相交于点 O,∠ACB 的角平分线分别交 AB、BD于 M、N 两点,若 AM=2,则线段 ON 的长为( ) A. B. C.1 D.3. 如图 9,在□ABCD 中,AC 与 BD 交于点 O,E 为 OD 的中点,连接 AE 并延长交 DC 于点F,则 DF∶FC 等于( )A.1∶4 B.1∶3 C.2∶3 D.1∶2图 7 图 8 图 9