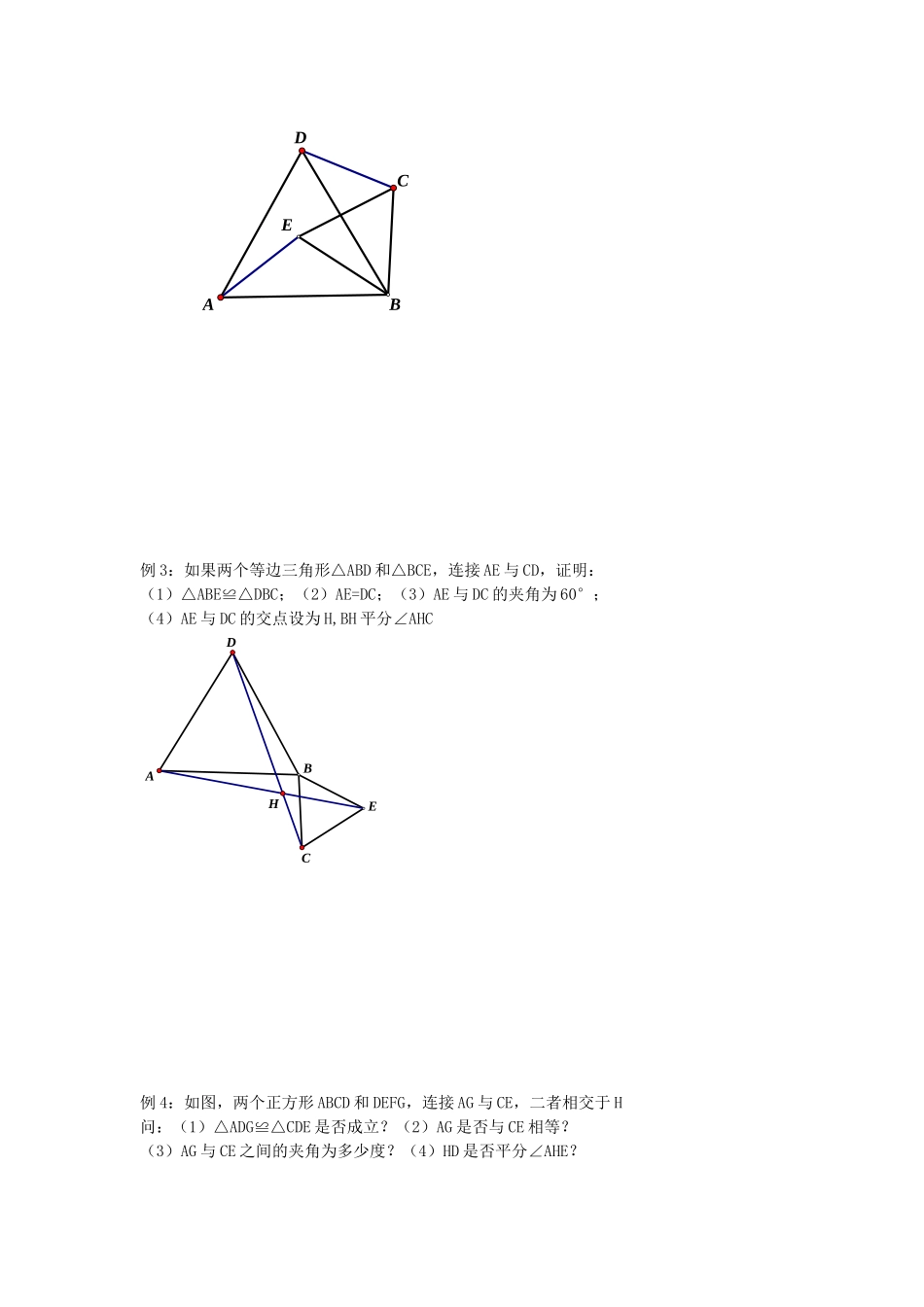
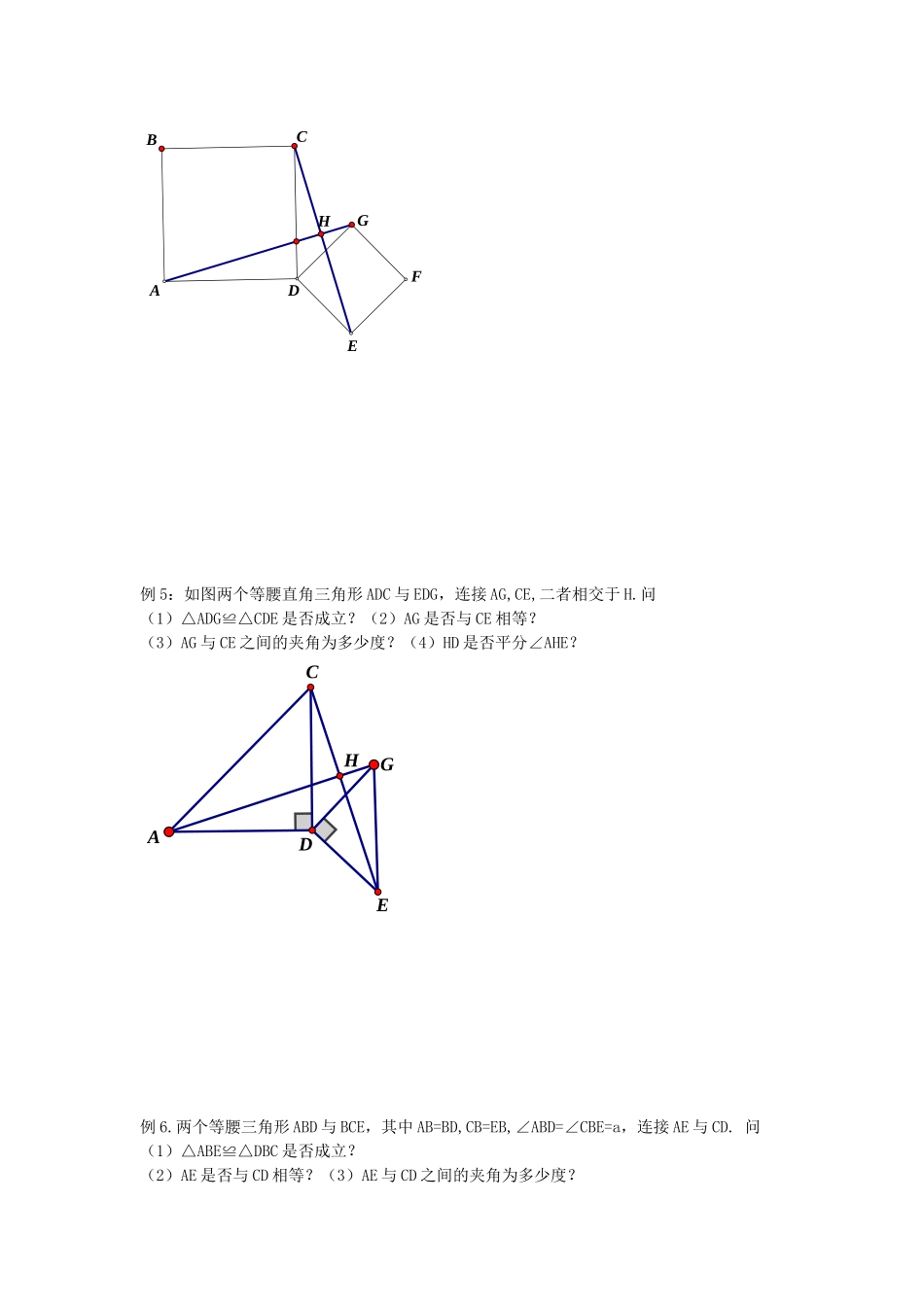
几何基本型研究——错位手拉手一、基本型回顾已 知 △ ABC 与 △ AED 中 AB=AC,AE=AD,BAC=EAD=90°∠∠图1、2、3 中分别有哪些结论把需要的全等和结论写在图形的边上.二、相应习题回顾例 1:在直线 ABC 的同一侧作两个等边三角形△ABD 和△BCE,连接 AE 与 CD,证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE 与 DC 的夹角为 60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)BH 平分∠AHC;GF∥ACHFGEDABC例 2:如果两个等边三角形△ABD 和△BCE,连接 AE 与 CD,证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE 与 DC 的夹角为 60°; (4)AE 与 DC 的交点设为 H,BH 平分∠AHCDCABEGDCABEGDCABEEBDAC例 3:如果两个等边三角形△ABD 和△BCE,连接 AE 与 CD,证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE 与 DC 的夹角为 60°;(4)AE 与 DC 的交点设为 H,BH 平分∠AHCHEBDAC例 4:如图,两个正方形 ABCD 和 DEFG,连接 AG 与 CE,二者相交于 H问:(1)△ADG≌△CDE 是否成立?(2)AG 是否与 CE 相等?(3)AG 与 CE 之间的夹角为多少度?(4)HD 是否平分∠AHE?HEFADBCG例 5:如图两个等腰直角三角形 ADC 与 EDG,连接 AG,CE,二者相交于 H.问 (1)△ADG≌△CDE 是否成立?(2)AG 是否与 CE 相等?(3)AG 与 CE 之间的夹角为多少度?(4)HD 是否平分∠AHE?HGADCE例 6.两个等腰三角形 ABD 与 BCE,其中 AB=BD,CB=EB,∠ABD=∠CBE=a,连接 AE 与 CD. 问(1)△ABE≌△DBC 是否成立?(2)AE 是否与 CD 相等?(3)AE 与 CD 之间的夹角为多少度?(4)HB 是否平分∠AHC?HDABCE7.在△ABC 中,AB=AC,∠BAC=90°,点 D 在 CB 上,连接 AD,EA⊥AD,∠ACE=∠ABD.若点 F 为CD 中点,AF 交 BE 于点 G,∠CBE=15°,AG=3√2则 BC 的长为 .GFDCABE三、错位手拉手基本型初探已知△ABC 与△AED 中 AB=AC,AE=AD,BAC=EAD=90°∠∠连接 BD、CE,AF 交 BD 于 F,交 EC 于 G.(1) 若 G 是 EC 中点,求证:AF 垂直 BD(2) 若 AF 垂直 BD,求证:EG=GC.GFDCABE(3) 若 G 是 BE 中点求证:AFCD⊥(4) 若 AFCD⊥求证:BG=GE四、基本型旋转再探(5) 若 G 是 CE 中点求证:AFBD⊥(6) 若 AFBD⊥求证:CG=GEGFDCABEGFECDBAGFDCABEGFECDBA五、方法迁移如图 1、已知△ABC 是等边三角形,△ADE 中 AD=AE,且∠DAE=120°连接 BE、DC,BE、DC 交于点 H,G 是 DC 中点连接 AG 并延长交 BC 于点 P,求证 AH=PC如图 2 已知△ABC 是等边三角形,△ADE 中 AD=AE,且∠DAE=120°连接 BE、DC.Q 是 BE 中点连接 AQ 并延长交 DC 于点 R,若 ADDC,⊥求证:AR=2DRHPFGEBACDRQHEBACD