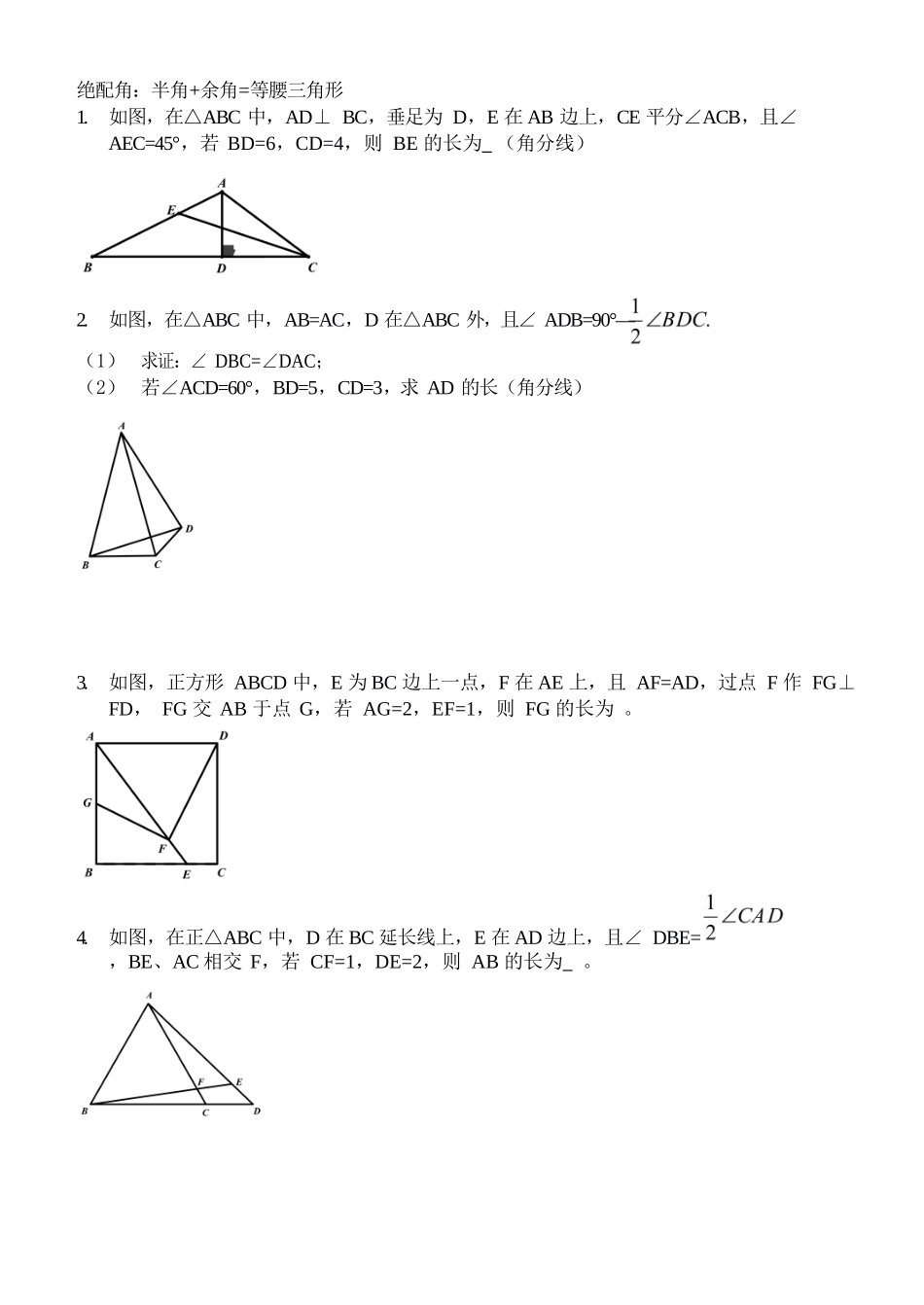
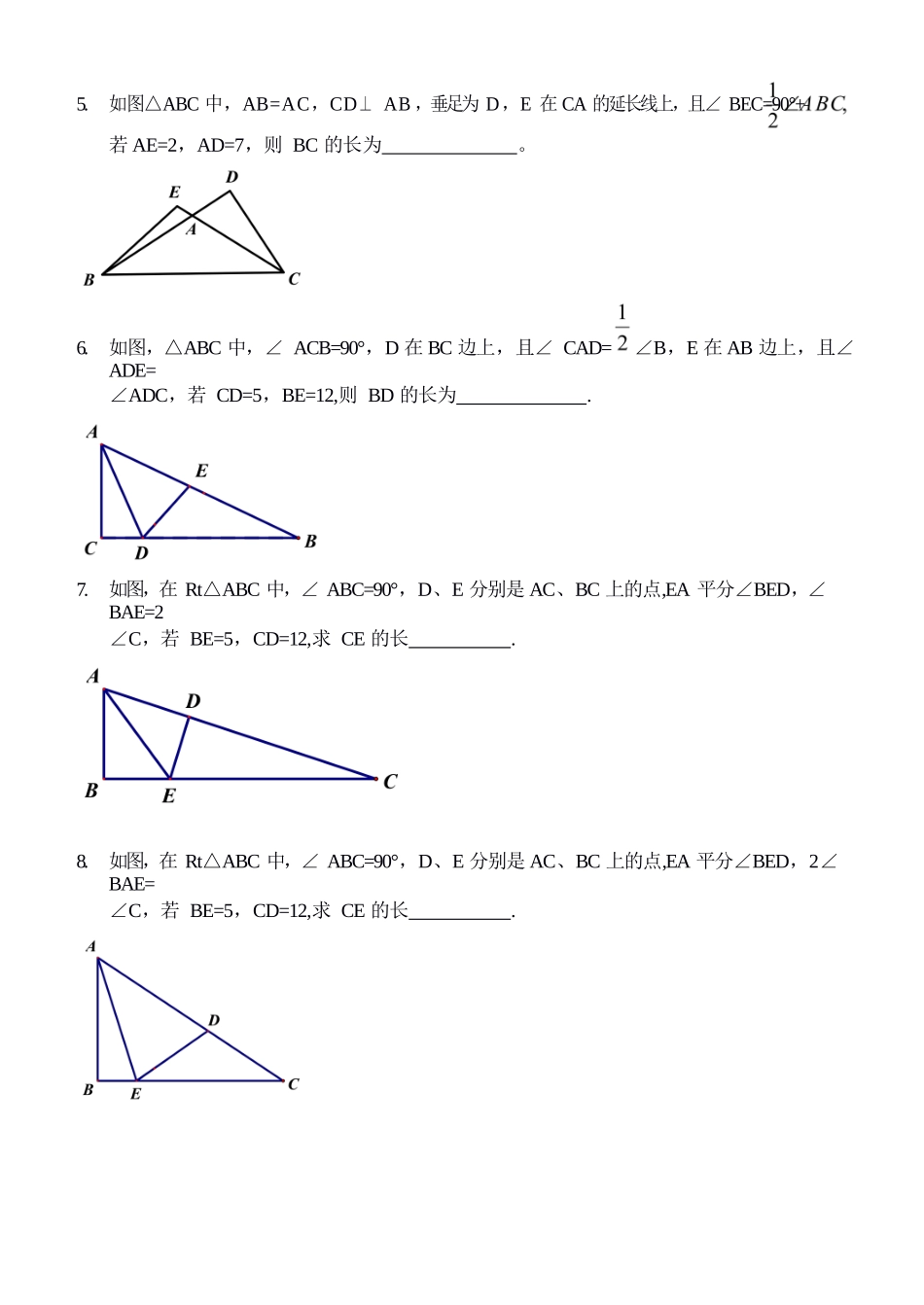
绝配角:半角+余角=等腰三角形1.如图,在△ABC 中,AD⊥ BC,垂足为 D,E 在 AB 边上,CE 平分∠ACB,且∠ AEC=45°,若 BD=6,CD=4,则 BE 的长为 (角分线)2.如图,在△ABC 中,AB=AC,D 在△ABC 外,且∠ ADB=90°—(1)求证:∠ DBC=∠DAC;(2) 若∠ACD=60°,BD=5,CD=3,求 AD 的长(角分线)3.如图,正方形 ABCD 中,E 为 BC 边上一点,F 在 AE 上,且 AF=AD,过点 F 作 FG⊥ FD, FG 交 AB 于点 G,若 AG=2,EF=1,则 FG 的长为 。4.如图,在正△ABC 中,D 在 BC 延长线上,E 在 AD 边上,且∠ DBE=,BE、AC 相交 F,若 CF=1,DE=2,则 AB 的长为 。5.如图△ABC 中,AB=AC,CD⊥ AB ,垂足为 D,E 在 CA 的延长线上,且∠ BEC=90°+若 AE=2,AD=7,则 BC 的长为 。6.如图,△ABC 中,∠ ACB=90°,D 在 BC 边上,且∠ CAD=∠B,E 在 AB 边上,且∠ ADE=∠ADC,若 CD=5,BE=12,则 BD 的长为 .7.如图,在 Rt△ABC 中,∠ ABC=90°,D、E 分别是 AC、BC 上的点,EA 平分∠BED,∠ BAE=2∠C,若 BE=5,CD=12,求 CE 的长 .8.如图,在 Rt△ABC 中,∠ ABC=90°,D、E 分别是 AC、BC 上的点,EA 平分∠BED,2∠ BAE=∠C,若 BE=5,CD=12,求 CE 的长 .