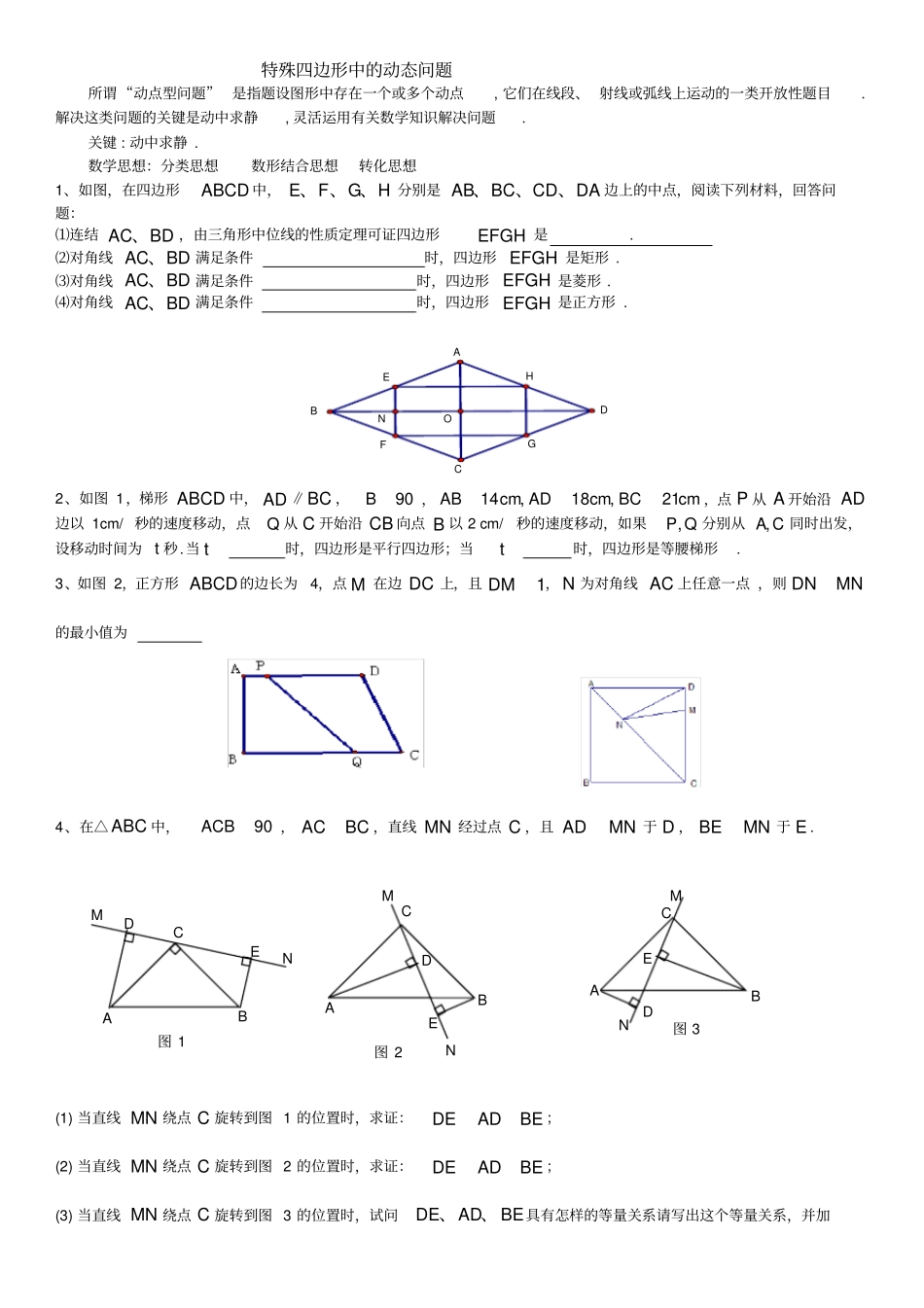
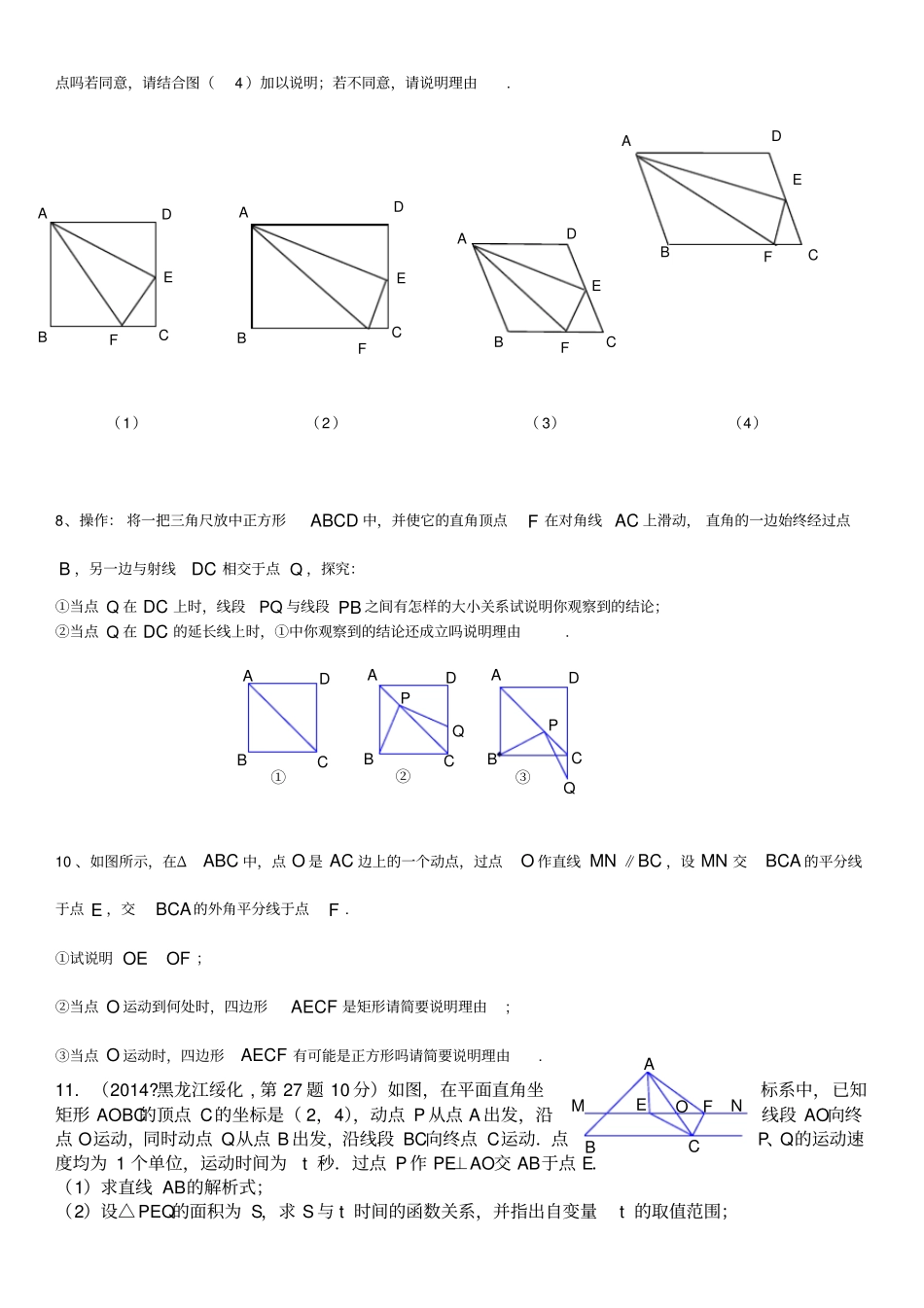
特殊四边形中的动态问题所谓“动点型问题” 是指题设图形中存在一个或多个动点, 它们在线段、 射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静, 灵活运用有关数学知识解决问题.关键 : 动中求静 .数学思想:分类思想数形结合思想转化思想1、如图,在四边形ABCD 中, EFGH、 、 、分别是 ABBCCDDA、、、边上的中点,阅读下列材料,回答问题:⑴连结 ACBD、,由三角形中位线的性质定理可证四边形EFGH 是 .⑵对角线 ACBD、满足条件时,四边形 EFGH 是矩形 .⑶对角线 ACBD、满足条件时,四边形 EFGH 是菱形 .⑷对角线 ACBD、满足条件时,四边形 EFGH 是正方形 .NOHGFEABCD2、如图 1,梯形 ABCD 中, AD ∥BC ,90B,14,18,21ABcm ADcm BCcm ,点 P 从 A 开始沿 AD边以 1cm/ 秒的速度移动,点Q 从 C 开始沿 CB 向点 B 以 2 cm/秒的速度移动,如果,P Q 分别从,A C 同时出发,设移动时间为 t 秒.当 t时,四边形是平行四边形;当t时,四边形是等腰梯形. 3、如图 2,正方形 ABCD的边长为4,点 M 在边 DC 上,且1DM, N 为对角线 AC 上任意一点 ,则 DNMN的最小值为4、在△ ABC 中,90ACB, ACBC ,直线 MN 经过点 C ,且 ADMN 于 D , BEMN 于 E . (1) 当直线 MN 绕点 C 旋转到图 1 的位置时,求证:DEADBE ;(2) 当直线 MN 绕点 C 旋转到图 2 的位置时,求证:DEADBE ;(3) 当直线 MN 绕点 C 旋转到图 3 的位置时,试问DEADBE、、具有怎样的等量关系请写出这个等量关系,并加C B A E D 图 1N M A B C D E M N 图 2A C B E D N M 图 3以证明 . 5、如图,在梯形ABCD 中,354 245ADBCADDCABB∥,,,,∠.动点 M 从 B 点出发沿线段BC 以每秒 2 个单位长度的速度向终点C 运动;动点 N 同时从 C 点出发沿线段 CD 以每秒 1 个单位长度的速度向终点 D 运动.设运动的时间为t 秒.(1)求 BC 的长.(2)当 MNAB∥时,求 t 的值.(3)试探究: t 为何值时,MNC△为等腰三角形.6、在矩形 ABCD中,204ABcmBCcm,,点 P 从 A 开始沿折线ABCD 以 4/cm s的速度运动,点 Q 从 C 开始沿 CD 边以 1/cm s 的速度移动,如果点PQ、分别从 AC、同时出发,当其中一点到达点D 时,另一点也随之停止运动,设运动时间为( )t s , t 为何值时,四边形APQD 也...