杨辉三角课件VIP免费

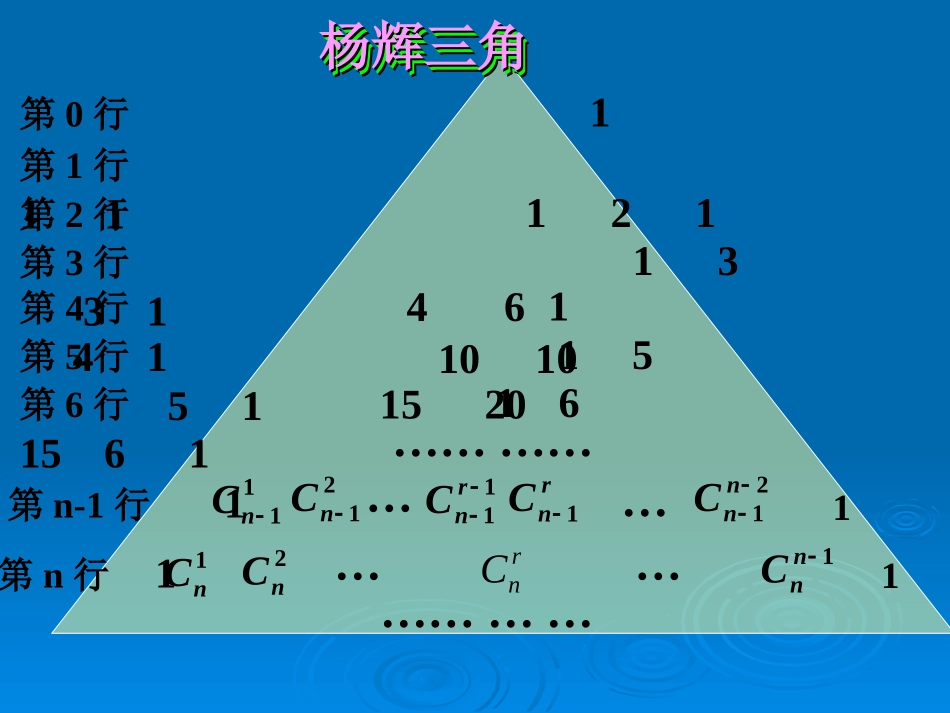
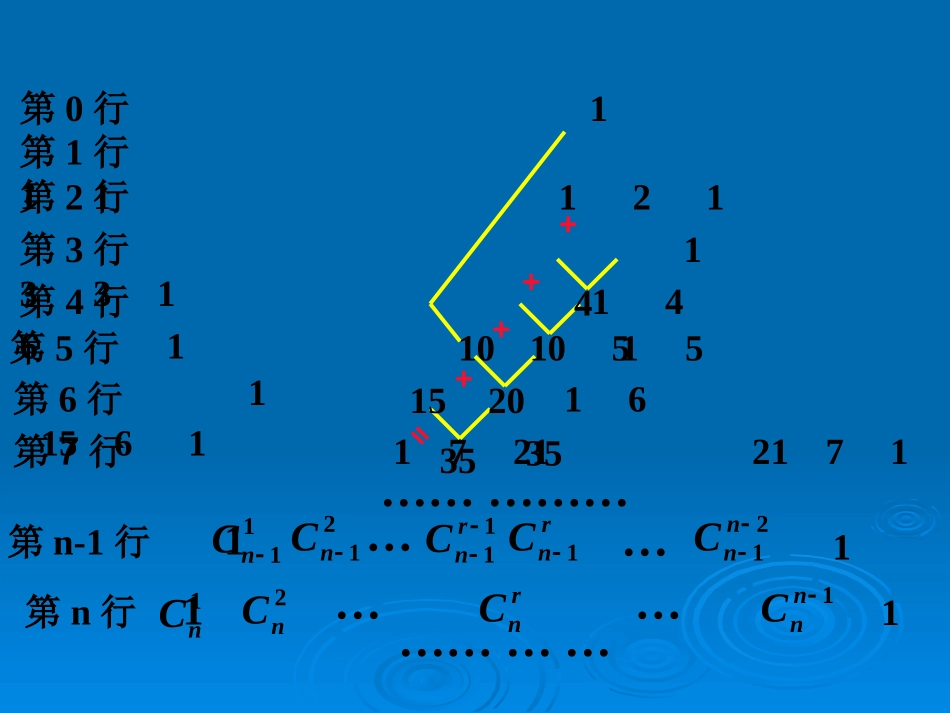
……第0行1第5行15101051第1行11第2行121第3行1331第4行14641第6行1615201561第7行172135352171第8行1828567056288111121nnrnnncccc第n行第5行1551第0行1杨辉三角杨辉三角杨辉三角杨辉三角第1行11第2行121第3行1331第4行141第6行161561第n-1行111nC121nC11rnCrnC121nnC第n行11nC12nC1nnC………………………………1520101064rnC第0行1第1行11第2行121第3行1331第4行1461第5行151第6行161561第n-1行111nC121nC11rnCrnC121nnC第n行11nC12nCrnC1nnC…………………………………第7行172121711035++++=3551520104斐波那契“兔子繁殖问题”斐波那契“兔子繁殖问题”中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题：假定一对刚出生的兔子一个月就能长成大兔子，再过一个月就开始生下一对小兔子，并且以后每个月都生一对小兔子．设所生一对兔子均为一雄一雌，且均无死亡．问一对刚出生的小兔一年内可以繁殖成多少对兔子？125第5行15101051第6行1615201561第7行172135352171第1行11第0行1第2行121第3行1331第4行14641……138132134如图，写出斜线上各行数字的和，有什么规律？第8行18285670562881从第三个数起，任一数都等于前两个数的从第三个数起，任一数都等于前两个数的和和;;这就是著名的这就是著名的斐波那契数列。斐波那契数列。杨辉三角与弹子游戏杨辉三角与弹子游戏在游艺场，可以看到如图的弹子游戏，小球(黑色)向容器内跌落，碰到第一层阻挡物后等可能地向两侧跌落，碰到第二层阻挡物再等可能地向两侧第三层跌落，如是，一直下跌，最终小球落入底层，根据具体区域获得奖品。试问：为什么两边区奖品高于中间区奖品？“概率三角形”12111824143838141218照这样计算第n+1层有n+1个通道，弹子通过各通道的概率将是？与杨辉三角有何关系？杨辉三角与“纵横路线图”杨辉三角与“纵横路线图”“纵横路线图”是数学中的一类有趣的问题：如图是某城市的部分街道图，纵横各有五条路，如果从A处走到B处(只能由北到南，由西向东)，那么有多少种不同的走法？AB由此看来，杨辉三角与纵横路线图问题有天然的联系3:2第0行1第1行11第2行121第3行1331第4行14641第5行15101051………………（04.上海春季高考）如图，在由二项式系数所构成的杨辉三角形中，第_____行中从左至右第14与第15个数的比为练习练习34通过“杨辉三角”了解古代数学家杨辉，通过“弹子游戏”了解现代数学家华罗庚，系统探究杨辉三角蕴含的数字排列规律及有关性质，培养观察、探究及创新能力。教学小结：教学小结：