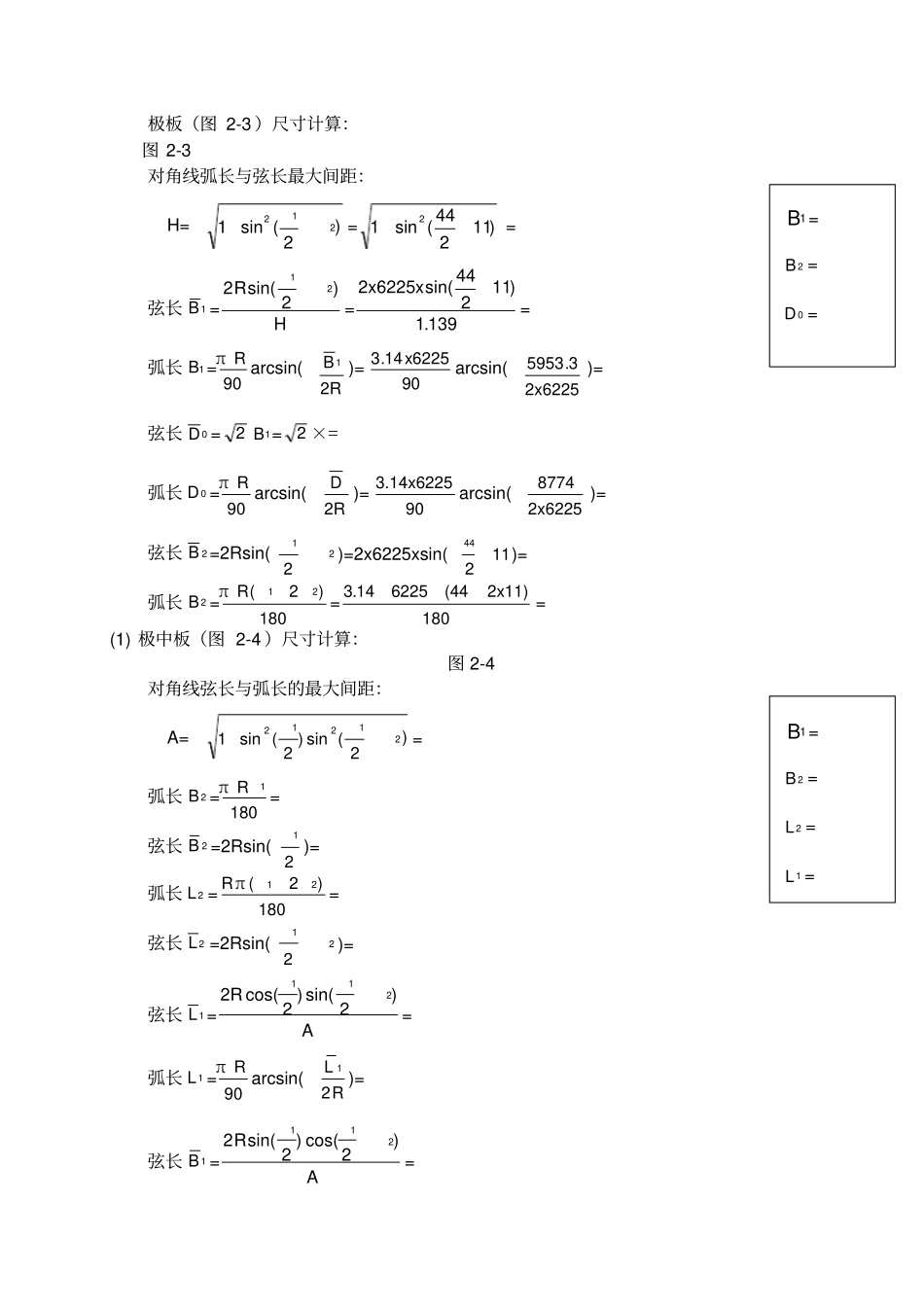
第二章 球罐结构设计球壳球瓣结构尺寸计算设计计算参数:球罐内径: D=12450mm 23341表P几何容积: V=974m3 公称容积: V1=1000m3球壳分带数: N=3支柱根数: F=8各带球心角 / 分块数:上极: ° /7赤道: ° /16 下极: ° /7图 2-1 混合式排板结构球罐混合式结构排板的计算:1. 符号说明: R-- 球罐半径 6225 mm N--赤道分瓣数 16 ( 看上图数的 ) α -- 赤道带周向球角°(360/16)0 -- 赤道带球心角 70°1 -- 极中板球心角 44°2-- 极侧板球心角 11°3 -- 极边板球心角 22°2 赤道板(图 2-2 )尺寸计算:图 2-2弧长 L =1800Rπ =18070622514.3= 弦长 L =2Rsin(20 )=2x6225×sin(270 )= 7141mm弧长1B =NRπ2cos(20 )=1614.362252x×cos270 =弦长1B =2Rcos(20 )sin(2)=2x6225×cos35sin25.22=弧长2B =NRπ2=1614.362252x=弦长2B =2Rsin2=2x6225×sin(25.22)=弦长 D =2R)2(cos)2(cos1202=2x6225x)25.22(cos)270(cos122 = 弧长 D =90Rπarcsin(2RD )=903.14x6225 arcsin(2x62257413.0 ) =1B = L = 极板(图 2-3 )尺寸计算:图 2-3对角线弧长与弦长最大间距: H=)2(sin1212=)11244(sin12 = 弦长1B =HR)2sin(221=139.1)11244sin(62252xx=弧长1B =90Rπarcsin(2RB 1 )=90622514.3xarcsin(2x62253.5953)=弦长0D =21B =2 ×=弧长0D =90Rπarcsin(2RD )=903.14x6225 arcsin(2x62258774)=弦长2B =2Rsin(212)=2x6225xsin(11244)=弧长2B =180)2(21Rπ=1802x11)(44622514.3=(1) 极中板(图 2-4 )尺寸计算:图 2-4对角线弦长与弧长的最大间距: A=)2(sin)2(sin121212=弧长2B =1801Rπ=弦长2B =2Rsin(21 )=弧长2L =180)2(R21π=弦长2L =2Rsin(212)=弦长1L =A)2sin()2cos(2R211=弧长1L =90Rπarcsin(RL21 )=弦长1B =AR)2cos()2sin(2211=1B = 2B =0D =1B = 2B =2L =1L =弧长1B =90Rπarcsin(2RB 1 )=弦长 D =2211BL=弧长 D =90Rπarcsin(2RD )=(2) 侧极板(图 2-5 )尺寸计算:图 2-5弦长1L =2Rcos(21 )sin(212)/A=弧长1L =90Rπarcsin (RL21 )=弦长2L =2Rsin(212)/H= 弧长2L =90Rπarcsin(RL22 )=K=2Rsin(21 )cos(212)/A=式中同前1 =arcsin(RL22 )-arcsin(2RK )=弧长2B =1802Rπ=弦长2B =2Rsin(22 )=弧长1B =1801πR=弦长 D =21LL1B=弧长 D =90Rπarcsin(2RD )=4. 极边板(图 2-6 )尺寸...