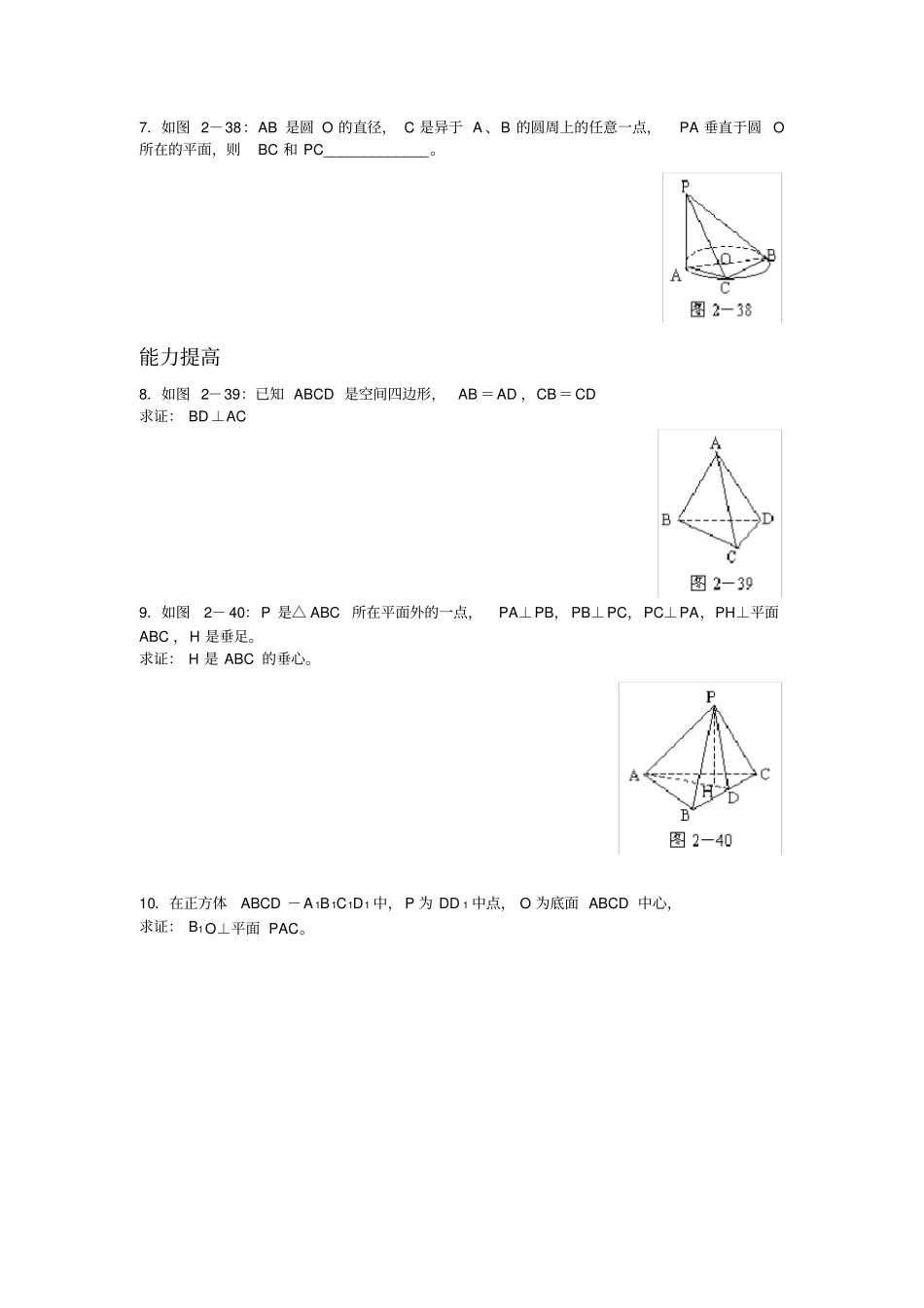
人教 A 版高中数学必修二第二章《2.3 直线、平面垂直的判定及其性质》练习题 1 2.3.1 直线与平面垂直的判定基础练习1.填空。(1) 过直线外一点可作_____条直线与该直线平行,可作______条直线与该直线垂直;(2) 过平面外一点可作_____条直线与该平面平行,可作______条直线与该平面垂直。2.一条直线与一个平面垂直的条件是( ) A. 垂直于平面内的一条直线B. 垂直于平面内的两条直线C. 垂直于平面内的无数条直线D. 垂直于平面内的两条相交直线3.如果平面α 外的一条直线a 与α 内两条直线垂直,那么( ) A. a⊥αB. a∥αC. a 与α 斜交D. 以上三种均有可能4.判断题:(对的打“√” ,错的打“×” )(3) 过已知直线外一点,有且只有一条直线与已知直线平行( ) (4) 过已知平面外一点,有且只有一条直线与已知平面平行( ) (5) 过一点有且只有一条直线与已知直线垂直( ) (6) 过一点有且只有一条直线与已知平面垂直( ) (7) 过一点有且只有一个平面与已知直线垂直( ) (8) 过已知直线外一点, 有且只有一个平面与已知直线平行。( ) 巩固练习5.如图 2-36:已知 PA⊥⊙ O 所在的平面, AB 是⊙ O 的直径,C 是异于 A 、B 的⊙ O 上任意一点,过A 作 AE ⊥PC 于 E,求证: AE⊥平面 PBC。6.图 2-37:BC 是 Rt△ABC 的斜边, AP⊥平面 ABC ,连结 PB、PC,作 PD⊥ BC 于 D,连结 AD ,则图中共有直角三角形_________个。7.如图 2-38:AB 是圆 O 的直径, C 是异于 A 、B 的圆周上的任意一点,PA 垂直于圆 O所在的平面,则BC 和 PC_____________。能力提高8.如图 2-39:已知 ABCD 是空间四边形,AB =AD ,CB=CD 求证: BD⊥AC 9.如图2- 40:P 是△ ABC所在平面外的一点,PA⊥PB, PB⊥PC,PC⊥PA,PH⊥平面ABC ,H 是垂足。求证: H 是 ABC 的垂心。10.在正方体ABCD -A 1B 1C1D1 中, P 为 DD 1 中点, O 为底面 ABCD 中心,求证: B1O⊥平面 PAC。答案基础练习1.1,无数;无数,1 2.D 3.D 4.√;×;×;√;√;×。巩固练习5.证明: PA⊥平面 ABC ,∴ PA⊥BC,又 AB 是⊙ O 的直径,∴ BC⊥AC 而 PA∩AC =A ,∴ BC⊥平面 PAC 又 AE平面 PAC,∴ BC⊥AE PC⊥AE 且 PC∩BC=C,∴ AE⊥平面 PBC。6.解: Rt△PAB、Rt△PAC、Rt△ABC 、Rt△ ADP。可证 BC⊥...