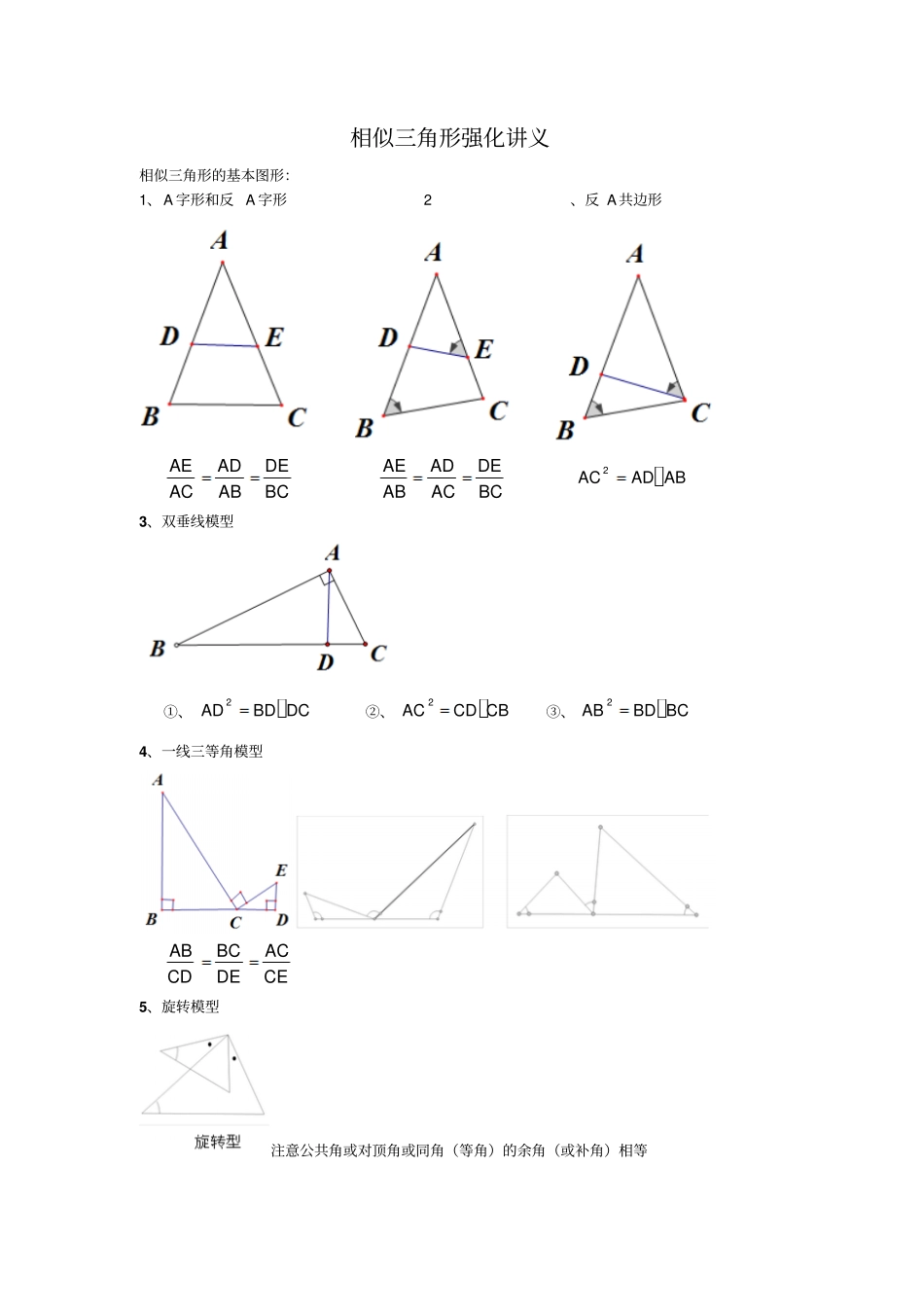
相似三角形强化讲义相似三角形的基本图形:1、A 字形和反 A 字形 2、反 A共边形AEADDEACABBCAEADDEABACBC2ACAD AB3、双垂线模型①、2ADBD DC②、2ACCD CB③、2ABBD BC4、一线三等角模型ABBCACCDDECE5、旋转模型注意公共角或对顶角或同角(等角)的余角(或补角)相等模块一:平行线分线段成比例1、(2015 年徐汇区一模) 如图,已知 ADBC∥,AC 与 BD 相交于点 O,点 G 是 BD 的中点,过点 G 作 GEBC∥交 AC 于点 E,如果1AD,3BC,那么:GE BC 等于⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()(A) 1: 2(B) 1:3(C) 1: 4(D) 2: 32、( 2014 年普陀区一模)已知D 、 E 分别是ABC的边 AB 、 AC 的上的点,DE ∥ BC ,若34BDAD,则BCDE 为()A .34;B.43 ;C.73 ;D.74 ;3、(2014 年长宁区一模)如图,四边形ABCD 的对角线 AC、BD 相交于点 O,且将这个四边形分成①、②、③、④四个三角形,若OA∶OC = OB∶OD,则下列结论中一定正确的是A .① 和 ② 相似; B.① 和 ③ 相似; C.① 和 ④相似; D.② 和④相似;()4、(2015 年闵行区一模) 如图,已知,D E 分别是△ ABC 的边 BC 和 AC 上的点,2AE,3CE,要使 DE ∥ AB ,那么:BC CD 应等于;5、( 2015 宝山区一模)在某一时刻,测得一根高为1.8m 的竹竿的影长为3m ,同时测得一根旗杆的影长为25m ,那么这根旗杆的高度为m ;6、( 2015 年闸北区一模如图5,在 Rt△ABC 中,∠ C= 90° ,点 D 在边 AB 上,线段 DC 绕点 D 逆时针旋转,端点C 恰巧落在边AC 上的点 E 处.如果mDBAD,nECAE.那么 m与 n 满足的关系式是:m=( 用含 n 的代数式表示m).7、(2014 年黄浦区一模). 如图 4,AB∥CD ∥EF ,如果:2:3AC CE,10BF,那么线段 DF 的长为 . 8、( 2014 年虹口区一模)如图,若AB∥ CD∥EF ,则下列结论中,与ADAF相等的是A. ABEF;B. CDEF;C. BOOE;D. BCBE.9、( 2015 年宝山区一模)如图直角梯形ABCD 中, AD ∥ BC ,2CD, ABBC ,1AD,动点 M 、 N 分别在 AB 边和 BC 的延长线运动,而且AMCN ,联结 AC 交MN 于 E , MH ⊥ AC 于 H ,则 EH;10、(2014 年闵行区一模)已知:如图,在平行四边形ABCD 中, E、F 分别是边 BC、CD上的点,且EF∥BD,AE、AF 分别交 BD 于点 G 和点 H,BD=12,EF=8.求...