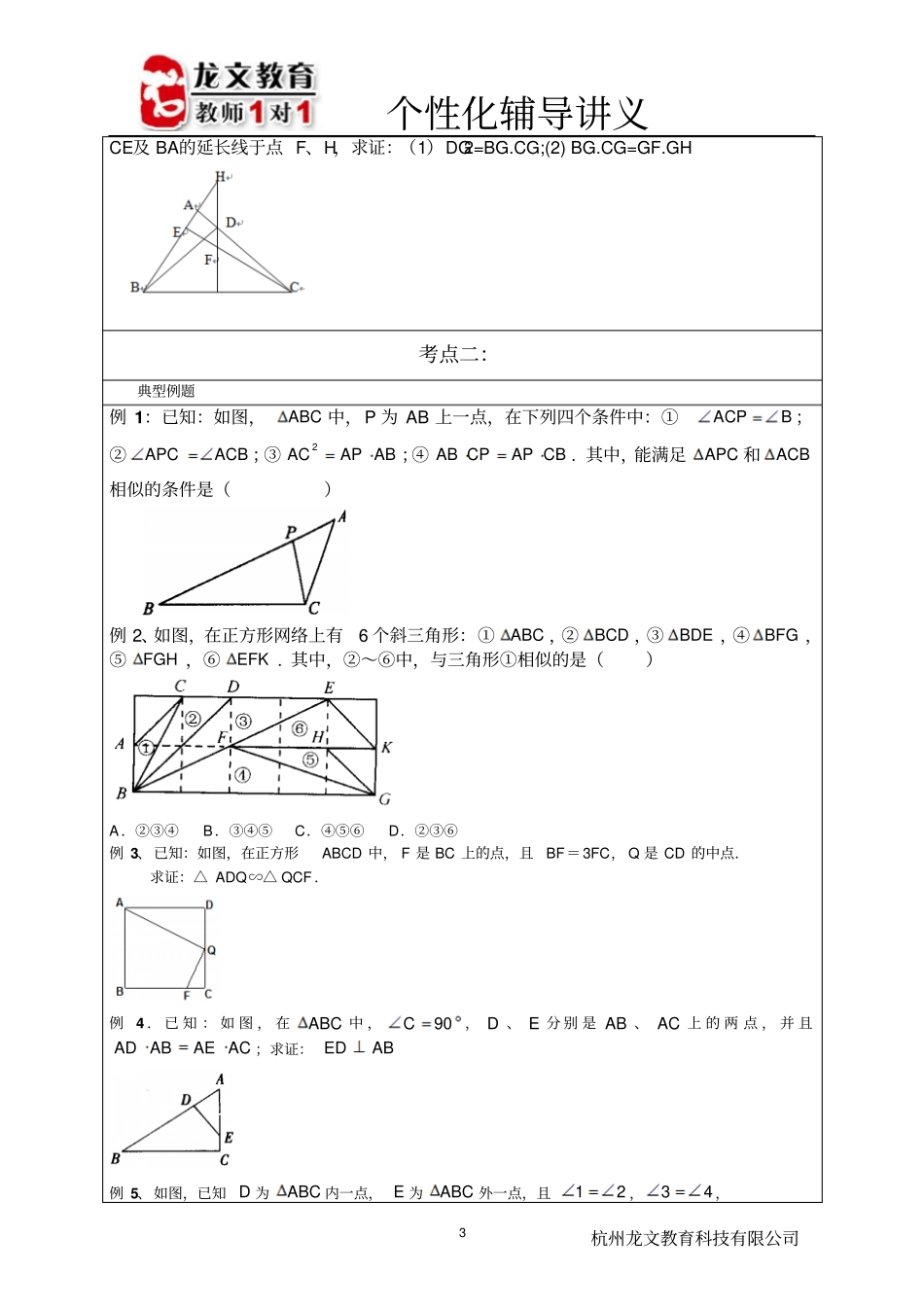
个性化辅导讲义杭州龙文教育科技有限公司1 课题两个三角形相似的判定教学目标1、理解并掌握两个相似三角形判定的方法2、能灵活应用四种判定方法判定两个三角形相似,并能结合相似三角形的性质进行证明3、培养学生的观察、动手探究及归纳总结的能力重点、难点能灵活应用四种判定方法判定两个三角形相似,并能结合相似三角形的性质进行证明教学内容知识框架相似三角形的判定方法:1、有两个角对应相等的三角形相似2、 平行于三角形一边的直线和其他两边相交所构成的三角形与原三角形相似3、 两边对应成比例,且夹角相等的两个三角形相似4、 三边对应成比例的两个三角形相似考点一:典型例题例 1、如图,平行四边形ABCD 中, G 是 BC 延长线上一点,AG 与 BD 交于点 E,与 DC 交于 F,则图中相似三角形共有对. 例 2、已知圆的两条弦BA、DC 的延长线交于点F,ADBC 交于点 E,求证:(1)△ ABE ∽△ CDE ;(2)FA.FB=FC.FD 例 3、在△ ABC 中, AC=AB, ∠A=36° , BD 是∠ ABC 的平分线,求证:(1)△ ABC ∽△ BCD ;(2)BC 是 CD 与 CA 的比例中项个性化辅导讲义杭州龙文教育科技有限公司2 例 4、如图,在△ ABC中,∠ABC=60° ,点 P是△ABC内的一点,且∠ APB=∠APC=∠BPC,PA=8,PC=6,则 PB=( ) 例 5、如图,在△ ABC中,AB=AC,AD是中线, P 是 AD上的一点,过点 C作 CF∥AB,延长 BP交 AC于点 E,交 CF于点 F,求证: BP2=PE.PF 针对性练习1.如图,在ABCRt中,90ACB,ACEFAF,4交 AB 于 E,ABCD,垂足为 D,若6CD,3EF,则 ED_______, BC_______, AB________. 2、△ABC内接于⊙ 0,∠ BAC的平分线 AD分别交 BC、⊙ 0 于点 E、D,连结 BD,根据已知条件,找出图中的各对相似三角形加以证明。3、点 F 是四边形 ABCD对角线 AC上的一点,EF∥BC,FG∥AD,求证:1CDCGABAE4、如图, BD、CE 分别是△ ABC的两边上的高,过点D作 DG⊥BC,垂足为 G,分别交个性化辅导讲义杭州龙文教育科技有限公司3 CE及 BA的延长线于点 F、H,求证:(1)DG2=BG.CG;(2) BG.CG=GF.GH考点二:典型例题例 1:已知:如图,ABC 中,P 为 AB 上一点,在下列四个条件中:①BACP;②ACBAPC;③ABAPAC2;④CBAPCPAB. 其中,能满足APC 和ACB相似的条件是()例 2、如图,在正方形网络上有6 个斜三角形:①ABC ,②BCD ,③BDE ,④BFG ,⑤FGH ,⑥EFK ....