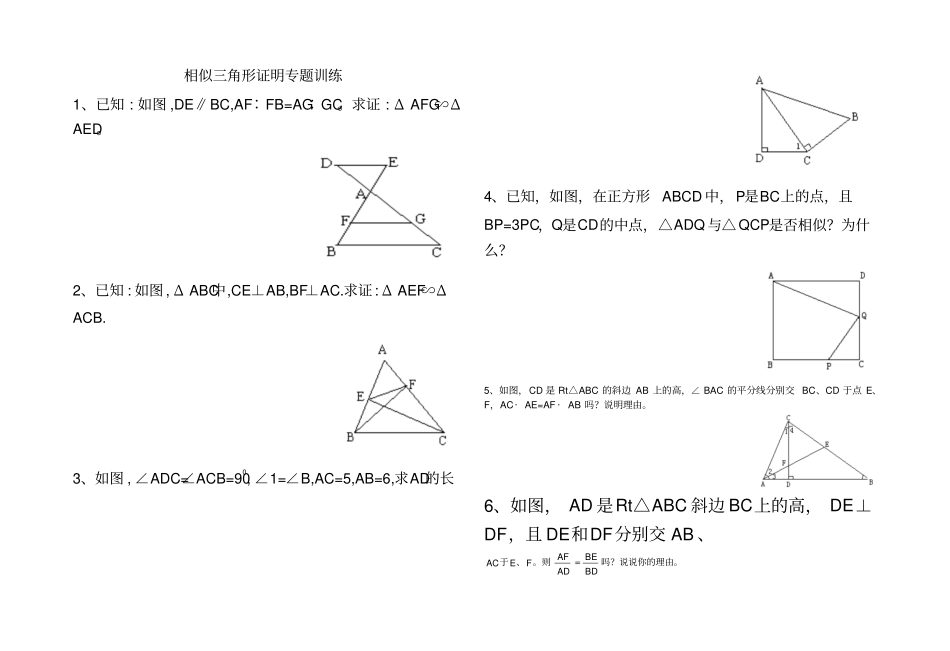
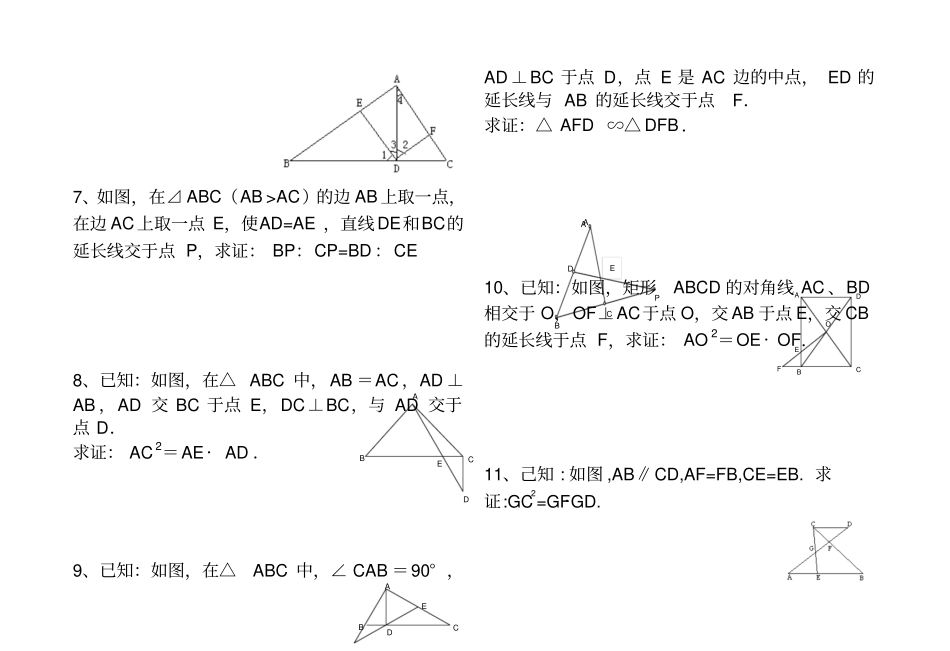
相似三角形证明专题训练1、已知 : 如图 ,DE∥BC,AF∶FB=AG∶GC。求证 : Δ AFG∽ΔAED。2、已知 : 如图, Δ ABC中,CE⊥AB,BF⊥AC.求证: Δ AEF∽ΔACB. 3、如图 , ∠ADC=∠ACB=900, ∠1=∠B,AC=5,AB=6,求AD的长4、已知,如图,在正方形ABCD 中,P是BC上的点,且BP=3PC,Q是CD的中点,△ADQ 与△QCP是否相似?为什么?5、如图,CD 是 Rt△ABC 的斜边 AB 上的高,∠ BAC 的平分线分别交 BC、CD 于点 E、F,AC· AE=AF · AB 吗?说明理由。6、如图, AD 是Rt△ABC 斜边 BC上的高, DE⊥DF,且 DE和DF分别交 AB 、ACEFAFADBEBD于、。则吗?说说你的理由。E AABPDC7、如图,在⊿ ABC(AB >AC)的边 AB 上取一点,在边 AC上取一点 E,使AD=AE ,直线 DE和BC的延长线交于点 P,求证: BP:CP=BD :CE 8、已知:如图,在△ ABC 中,AB =AC ,AD ⊥AB ,AD 交 BC 于点 E,DC⊥BC,与 AD 交于点 D.求证: AC 2=AE· AD .9、已知:如图,在△ABC 中,∠ CAB =90° ,AD ⊥BC 于点 D,点 E 是 AC 边的中点, ED 的延长线与 AB 的延长线交于点F.求证:△ AFD ∽△ DFB .10、已知:如图,矩形ABCD 的对角线 AC 、BD相交于 O,OF⊥AC于点 O,交 AB 于点 E,交 CB的延长线于点 F,求证: AO 2=OE · OF.11、己知 : 如图 ,AB∥CD,AF=FB,CE=EB. 求证:GC2=GF·GD. B C D A E B C D A F E O B C D A E 12、已知 : 如图 , Δ ABC中, ∠ACB=900,F 为AB的中点,EF⊥AB.求证 : Δ CDF∽Δ ECF. 13、已知 : 如图 ,DE∥BC,AD2=AF·AB。求证 : Δ AEF∽Δ ACD。14、已知 : 如图 , Δ ABC中, ∠ABC=2∠C,BD平分∠ABC.求证 :AB·BC=AC·CD. 15、已知 : 如图 , Δ ABC中,AD=DB,∠1=∠2. 求证 :Δ ABC∽Δ EAD. 16、已知 : 如图 , ∠1=∠2, ∠3=∠4. 求证 : Δ DBE∽Δ ABC. 17、已知,如图,在平行四边形ABCD 中, E为 AC 三分之一处, 即 AE = 31 AC,DE 的延长线交 AB 于 F,求证: AF = FB DABCFE18、如图,∠ B=90 0,AB=BE=EF=FC=1 。求证:Δ AEF∽Δ CEA. 19、如图,在梯形ABCD中, AB ⊥ BC ,∠BAD=90 ° ,对角线BD ⊥DC。(1)△ABD 与△ DCB 相似吗?请说明理由。(2)如果 AD=4 ,BC=9,求 BD的长。20、已知 :如图,在△ PAB 中,...