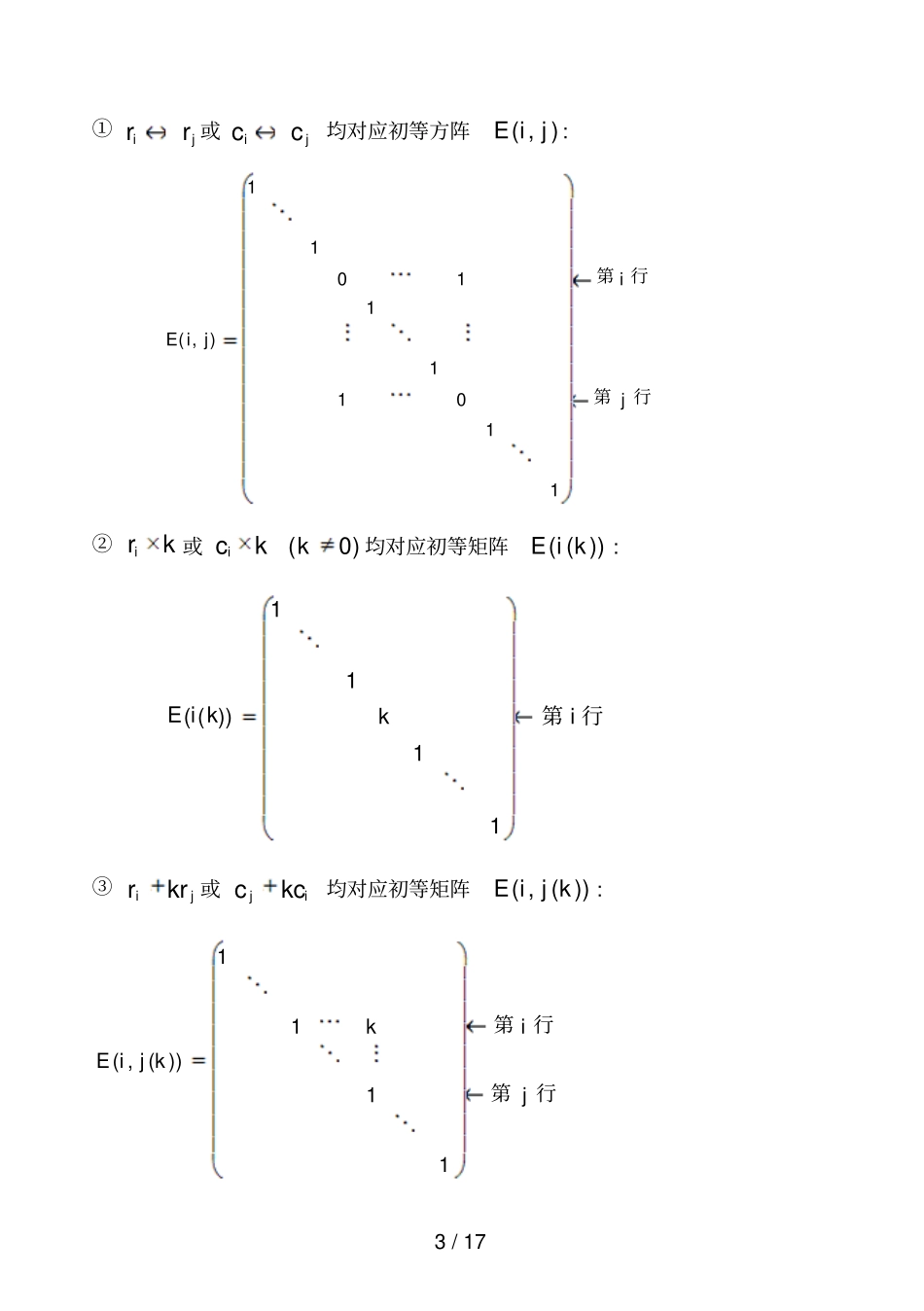
1 / 17 第三讲 矩阵的初等变换一、概念1. 定义矩阵的初等变换:下面的三种变换称为矩阵的初等变换(1) jirr;jicc. (换行或换列)(2) kri;kci(数0k)(倍行或倍列)(3) jikrr;jikcc.. (倍行加或倍列加)2. 矩阵 A 与 B 等价 :nmA经过有限次的初等变换变成B . 记作~AB . (1)等价的性质:反身性~AA ;对称性若~AB ,则~BA ;传递性若~,~AB BC ,则~AC . (2)任何矩阵nmA都等价于一个标准形矩阵, 即()()() ()( )r rrn rm nm nn rrn rn rEOAFrOO.即存在有限个初等矩阵lPPP,,,21, 使121( )kklm nPPP APPFr.且矩阵的等价标准形惟一确定 . (3)行阶梯矩阵 :可画出一条阶梯线,线的下方全是零;每个台阶只有一行,台阶数为非零行的行数,阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元,即非零行的第一个非零元. 例如1210104112140110301113,00013000130000000000AA上述两矩阵均为行阶梯矩阵. 2 / 17 (4)行最简形矩阵 :非零行的非零首元为1,且这些非零元所在的列的其他元素都为零的行阶梯矩阵. 110104011030001300000A为行最简形矩阵. 例 1求所给矩阵A 的行阶梯矩阵、行最简形矩阵以及等价标准型矩阵. 123221112112141121421112~46224231123697936979rrrA4221323141r222311214112140331603316~05536011160334300039~rrrrrrrrr2333243r3( 4)311214112140111601116000412000130003900000~~rrrrrr(行阶梯矩阵)1232321010401103~0001300000rrrrr3151325254344334 51000001000~0010000000ccccccccccccF.(行最简形矩阵)(等价标准型矩阵)3. 初等矩阵的概念(1)定义初等矩阵 :由 单位矩阵 E 只经过一次初等变换得到的方阵 . 3 / 17 ①jirr或jicc均对应初等方阵),(jiE: 行第行第jijiE1101111011),(②kri或kci)0(k均对应初等矩阵))(( kiE:行第 ikkiE1111))((③jikrr或ijkcc均对应初等矩阵))(,(kjiE:行第行第jikkjiE1111))(,(4 / 17 (2)初等矩阵行列式的性质( , )1;( ( ))(0);( , ( ))1E i jE i kk kE i j k . 重要结论 :初等矩阵是可逆矩阵,且逆矩阵仍然是初等矩阵. (3) 初等矩阵的逆矩阵①),(),(1jiEjiE; ②))1(())((1kiEkiE, )0(k; ③))(,())(,(1kjiEkjiE. (4) 初等矩阵的转置也是初等矩阵. ①),(),(jiEjiET; ②))(())((kiEkiET, )0(k; ③))(,())(,(kijEkjiET. 4. 矩阵初等变换的重要性质【性质 1】 设 A...