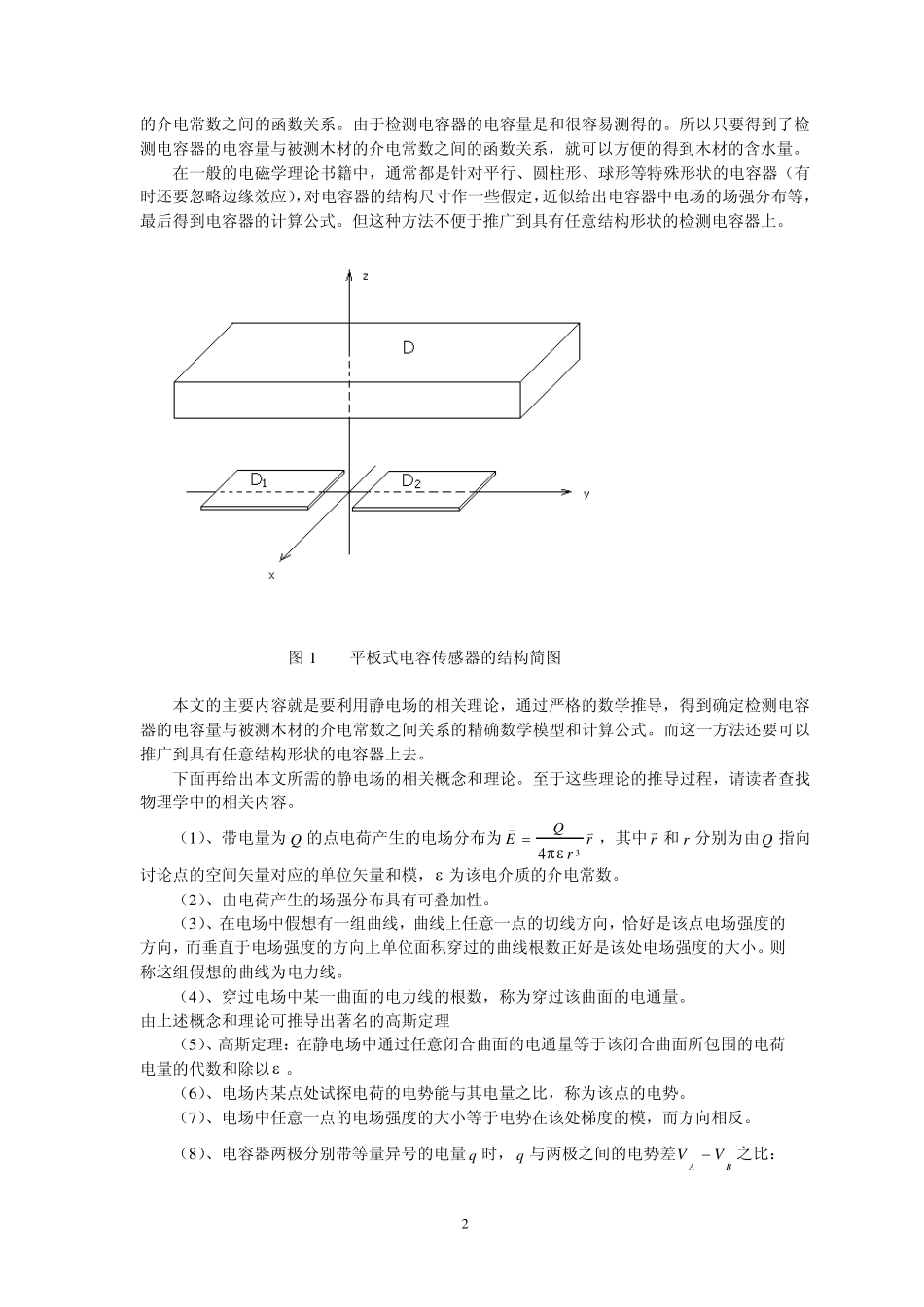
1 平板式电容传感器的工作原理和数学模型 大家都知道,在电容器中加入不同的电介质,会使得电容器有不同的电容量。利用这一性质,人们已经制造出了许多具有不同用途的电容传感器。诸如测量液位、压力、位移[1]、加速度、介电常数[2][3]、含水量[4][5]等的电容传感器都是利用电容器的这一特性制造的。它们通常具有体积小、结构简单、响应时间短、分辨率高等突出优点。而且由于检测头结构简单,所以能接受相当大的温度变化及各种辐射作用,可在强烈振动等恶劣条件下工作。 近些年来电容传感器受到人们的广泛关注,它是一类为较理想的检测仪器。本文将要研究的平板式电容传感器就属于电容传感器。 本文作者查阅了大量的关于电容传感器的相关文献。但发现虽然对于该类传感器的研究工作,已有一些文献发表,但多数研究工作是在对该类电容传感器所产生的静电场中电力线、电位等物理量的性质作了一定的人为假设的前提下进行的。而这些人为假设与实际情况都是有一定的差距的。所以得到的数学模型可以说都是些近似模型,所得结果也会有较大的误差,如[3]中近似地用半圆弧线代替电力线的真实曲线。[2]中用二维场中的拉普拉斯方程代替真实的三维空间的拉普拉斯方程来描述该类电容传感器所产生的静电场的电位分布。这样都会给研究结果带来误差。针对这一情况,本文作者已经在前期研究了电容传感器的普遍原理。利用静电场及场中导体和电介质、电容器等的相关理论,经过严密的数学推导,建立了该类电容传感器的精确的偏微分方程数学模型,来确定检测电容影响的静电场的电势。但是当被测物体的形状、检测电容的两极的形状为任意的形状时,所建偏微分方程模型的精确解往往难以求得。通常可用数值计算得到其近似解,再利用所求近似解对该类电容传感器的工作状况进行研究。 本文将介绍的平板式电容传感器是用来测量木材含水率的高精度仪器。由于象木材这样的电介质的含水量可直接影响电介质的介电常数。在一定的条件下木材的介电常数可以被它的含水量惟一确定,并且介电常数和含水量的对应关系是一对一的,所以在特定的条件下可以利用该电容传感器先测量出木材的介电常数,再间接地得到木材的含水量。 本文以一种特殊尺寸的平板式电容传感器为例,利用数值分析的方法对本文所建立的偏微分方程数学模型,构造了便于计算和研究的离散近似模型。利用该近似模型对该类电容传感器的工作状况进行了论分析,得到了相关结论。文中所用方法可以方便地推广到具有一般尺寸...