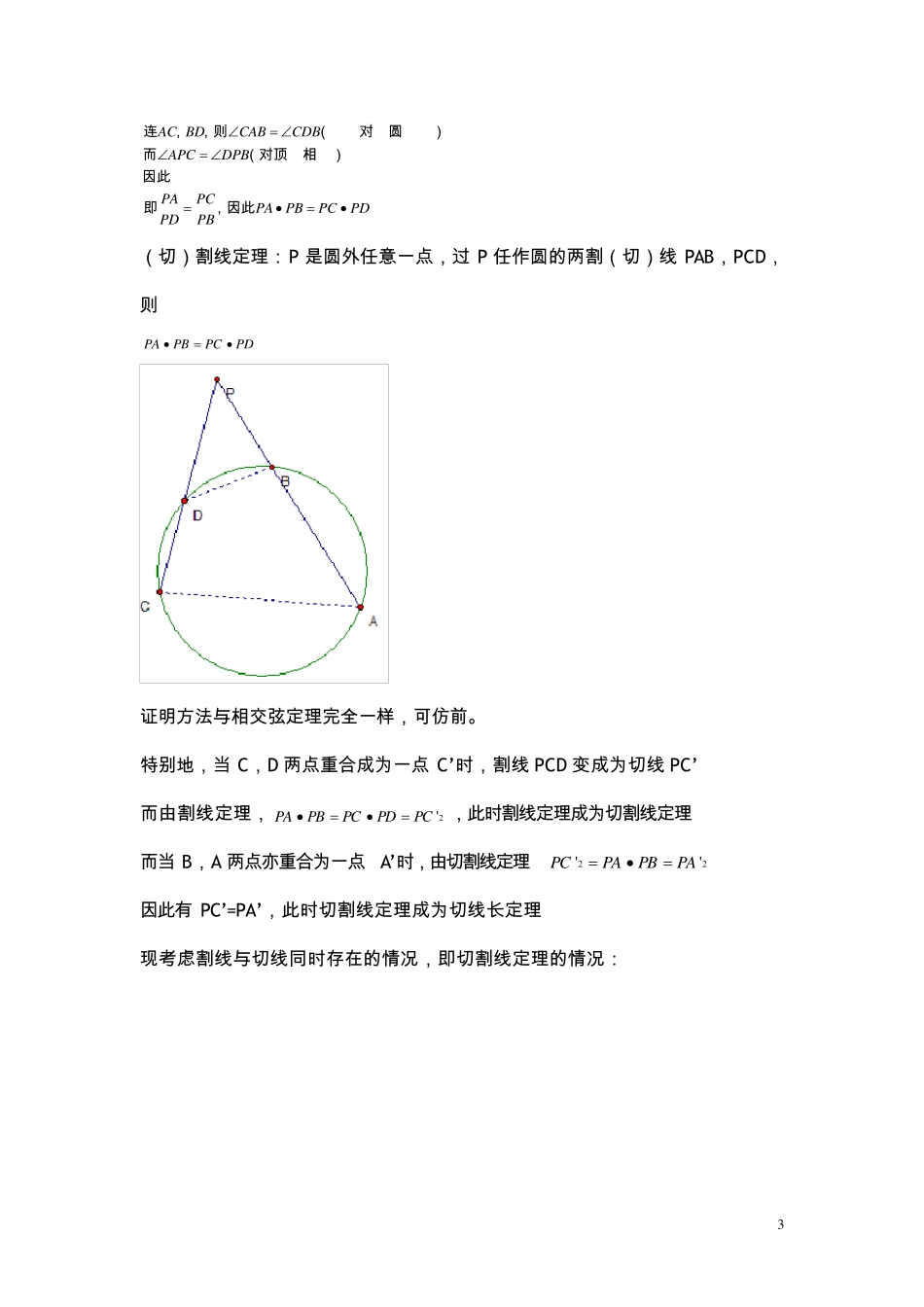
1 平 面 几 何 基 础 知 识 教 程 ( 圆 ) 一 、 几 个重要定义 外心:三角形三边中垂线恰好交于一 点,此点称为外心 内心:三角形三内角平 分线恰好交于一 点,此点称为内心 垂心:三角形三边上的高所在直线恰好交于一 点,此点称为垂心 凸四边形:四边形的所有对角线都在四边形 ABCD 内部的四边形称为凸四边形 折四边形:有一 双对边相交的四边形叫做折四边形( 如下图) ( 折四边形) 二、 圆 内重要定理: 1. 四点共圆 定义:若四边形 ABCD 的四点同时共于一 圆 上,则称 A,B,C,D 四点共圆 基 本性质:若凸四边形 ABCD 是圆 内接四边形,则其对角互补 证明:略 判定方法: 1.定义法:若存在一 点 O 使 OA=OB=OC=OD,则 A,B,C,D 四点共圆 2.定理 1:若凸四边形 ABCD 的对角互补,则此凸四边形 ABCD 有一 外接圆 证明:略 特别地,当凸四边形 ABCD 中有一 双对角都是 90 度时,此四边形有一 外接圆 3.视角定理:若折四边形 ABCD 中, ADBACB ,则 A,B,C,D 四点共圆 2 证 明 : 如 上 图 , 连 CD, AB, 设 AC 与 BD 交 于 点 P 因 为 ADBACB , 所 以 1 8 0 ΔCPB∽ΔDPA所 以 有再注意到因 此Δ∽Δ因 此由此(ΔABD的 内 角和)因 此A, B, C, D四 点 共圆PCPBPDPACPDBPACPDBPAPCDPBABCDBADBCAPCDBADBDAPBABAD 特 别 地 , 当 ADBACB =90 时 , 四 边 形 ABCD 有 一 外 接 圆 2. 圆 幂 定 理 : 圆 幂 定 理 是 圆 的 相 交 弦 定 理 、切割线定 理 、割线定 理 、切线长定 理 的 统一 形 式。 相 交 弦 定 理 : P 是 圆 内 任一 点 , 过 P 作圆 的 两弦 AB, CD, 则 PAPBPCPD•• 证 明 : 3 ••连,, 则( 等弧对 等圆 周角)而( 对 顶 角相 等)因 此 ΔAPC∽ΔDPB即, 因 此AC BDCABCDBAPCDPBPAPCPAPBPCPDPDPB ( 切 ) 割 线 定 理 : P 是 圆 外 任 意 一 点 , 过P 任 作 圆 的 两 割 ( 切 ) 线PAB, PCD,则 PAPBPCPD•• 证 明 方 法 与 相 交 弦 定 理 完 全 一 样 , 可 仿 前 。 特别地, 当 C, D 两 点 重合...