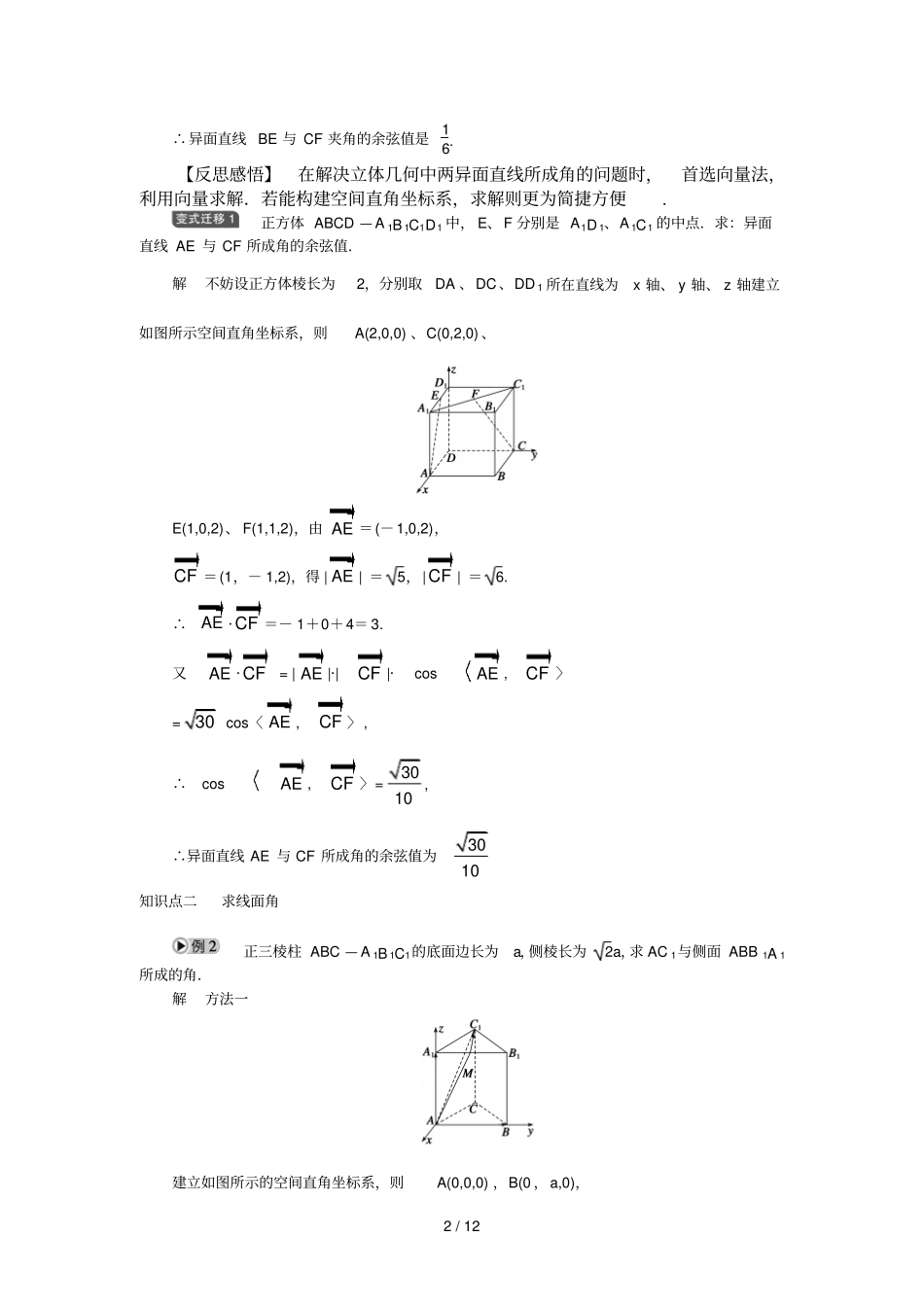
1 / 12 §3.2立体几何中的向量方法(二) ——利用向量方法求角知识点一求异面直线所成的角已知平行六面体ABCD — A 1B1C1D 1 的所有棱长都是1,且∠ A 1AB =∠ A 1AD=∠ BAD =60° ,E、F 分别为 A 1B1 与 BB 1 的中点,求异面直线BE 与 CF 所成角的余弦值.解如图所示,解 如图所示,设AB= a,AD= b,1AA= c.则| a | = | b | = | c | =1,〈 a,b 〉=〈b,c〉 =〈a,c 〉= 60,∴a·b = b·c = a·c = 12,而BE=1BB+1B E= 12a + c.CF= CB + BF= b + 12c,∴|BE | =14|a|2+|c|2-a·c =32 ,| CF | =32 . ∴ BE · CF= -12a+c · -b+12c=12a·b-14a·c-b·c+ 12c2=18,cos〈 BE , CF 〉=BECFBECF= 16 ,2 / 12 ∴异面直线 BE 与 CF 夹角的余弦值是16. 【反思感悟】在解决立体几何中两异面直线所成角的问题时,首选向量法,利用向量求解.若能构建空间直角坐标系,求解则更为简捷方便. 正方体 ABCD — A 1B 1C1D1 中, E、F 分别是 A1D 1、A 1C1 的中点.求:异面直线 AE 与 CF 所成角的余弦值.解不妨设正方体棱长为2,分别取DA 、DC 、DD 1 所在直线为x 轴、 y 轴、 z 轴建立如图所示空间直角坐标系,则A(2,0,0) 、C(0,2,0) 、E(1,0,2)、 F(1,1,2),由 AE =(-1,0,2),CF =(1,- 1,2),得 | AE | =5,|CF | =6. ∴AE ·CF =- 1+0+4= 3. 又AE ·CF= | AE |·|CF |·cosAE ,CF 〉=30 cos〈 AE ,CF 〉,∴cosAE ,CF 〉=3010,∴异面直线 AE 与 CF 所成角的余弦值为3010知识点二求线面角正三棱柱 ABC — A 1B 1C1的底面边长为a,侧棱长为2a,求 AC 1与侧面 ABB 1A 1所成的角.解方法一建立如图所示的空间直角坐标系,则A(0,0,0) ,B(0 ,a,0),3 / 12 A 1(0,0,2a),C1 -32 a,a2,2a ,取 A 1B 1 中点 M ,则 M 0,a2,2a ,连结 AM 、MC 1,有1MC = -32 a,0,0 , AB =(0, a,0),1AA =(0,0,2a),由于1MC ·AB = 0 ,1MC ·1AA = 0 ,∴MC1⊥面ABB1A1.∴∠C1AM是 AC1与侧面 A1B 所成的角θ . 1AC = -32 a,a2,2a , AM = 0,a2,2a ,∴1AC · AM =0+a24 +2a2=9a24 . 而|1AC | =3a24 + a24 +2a2=3a,| AM |=a24 +2a2=32a,∴cos〈1AC, AM 〉=9a243a×3a2=3...