线段和差最值问题

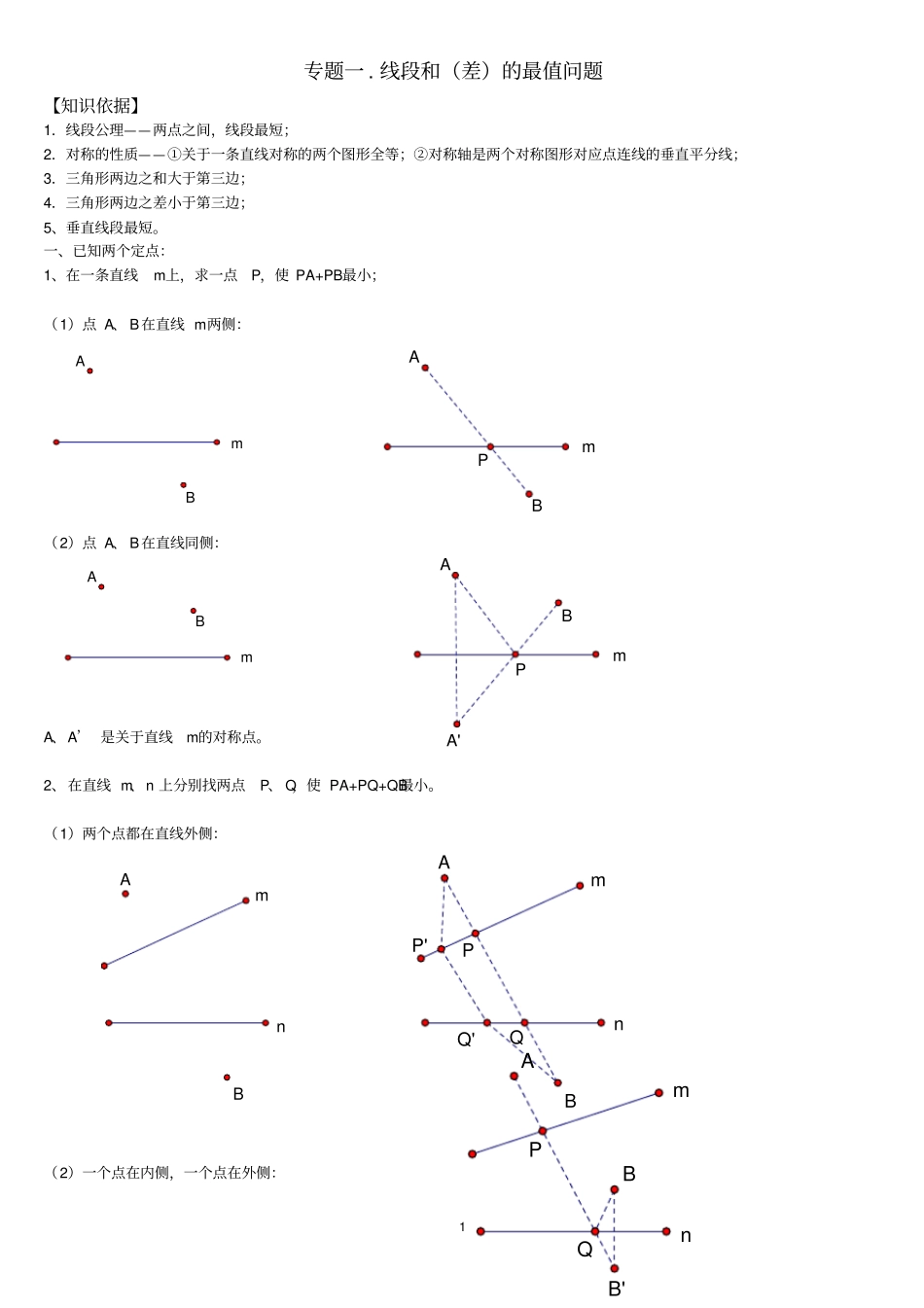
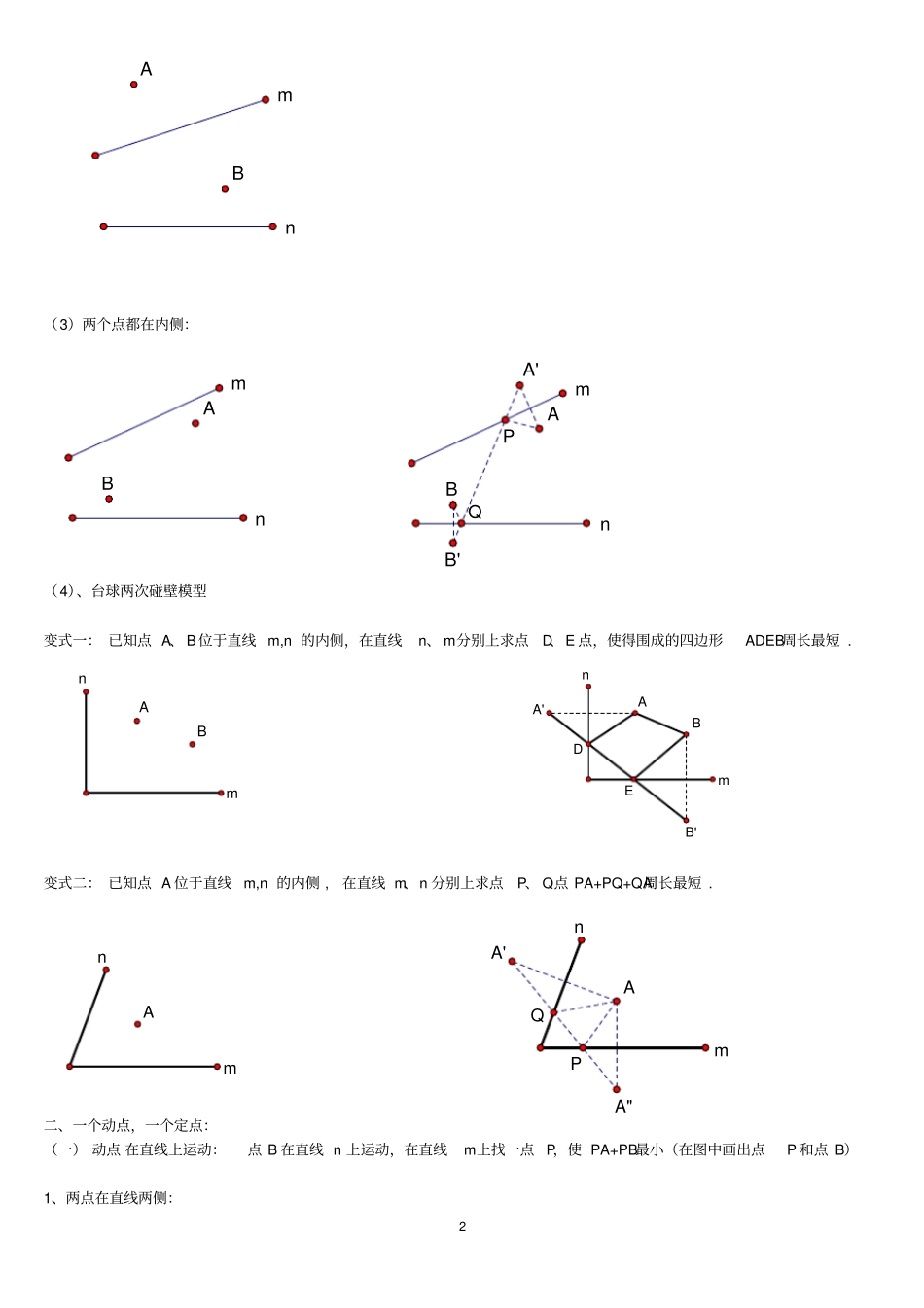
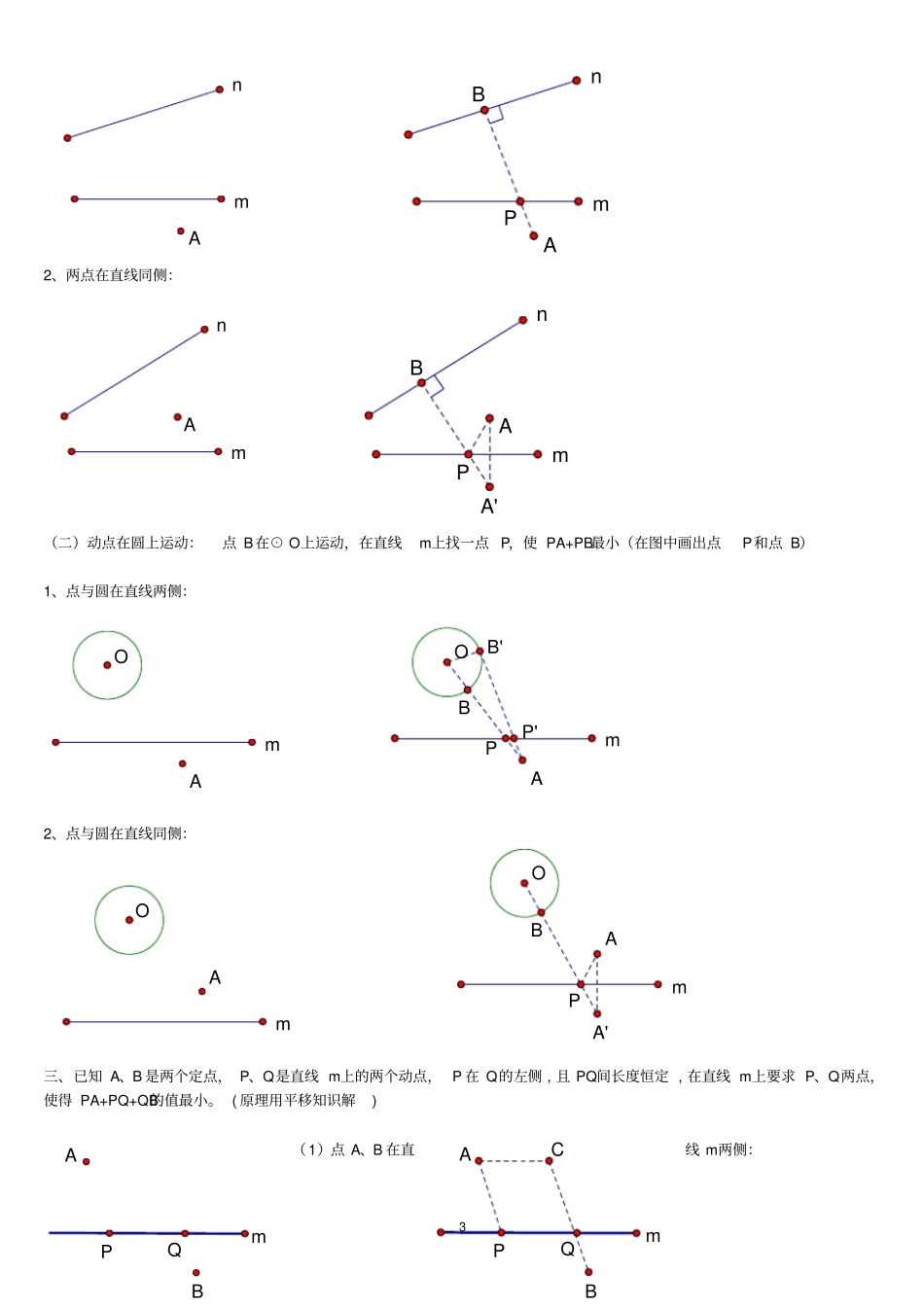
1专题一 . 线段和（差）的最值问题【知识依据】1．线段公理——两点之间，线段最短；2．对称的性质——①关于一条直线对称的两个图形全等；②对称轴是两个对称图形对应点连线的垂直平分线；3．三角形两边之和大于第三边；4．三角形两边之差小于第三边；5、垂直线段最短。一、已知两个定点：1、在一条直线m上，求一点P，使 PA+PB最小；（1）点 A、 B在直线 m两侧：（2）点 A、 B在直线同侧：A、A’ 是关于直线m的对称点。2、在直线 m、n 上分别找两点P、 Q，使 PA+PQ+QB最小。（1）两个点都在直线外侧：（2）一个点在内侧，一个点在外侧：PmABmABmABPmABA'nmABQPnmABP'Q'QPnmABB'2（3）两个点都在内侧：（4）、台球两次碰壁模型变式一： 已知点 A、 B位于直线 m,n 的内侧，在直线n、 m分别上求点D、E 点，使得围成的四边形ADEB周长最短 .变式二： 已知点 A 位于直线 m,n 的内侧 , 在直线 m、n 分别上求点P、 Q点 PA+PQ+QA周长最短 .二、一个动点，一个定点：（一） 动点 在直线上运动：点 B 在直线 n 上运动，在直线m上找一点 P，使 PA+PB最小（在图中画出点P 和点 B）1、两点在直线两侧：nmABQPnmABB'A'nmABmnABEDmnABA'B'mnAPQmnAA"A'32、两点在直线同侧：（二）动点在圆上运动：点 B在⊙ O上运动，在直线m上找一点 P，使 PA+PB最小（在图中画出点P和点 B）1、点与圆在直线两侧：2、点与圆在直线同侧：三、已知 A、B 是两个定点， P、Q是直线 m上的两个动点， P 在 Q的左侧 , 且 PQ间长度恒定 , 在直线 m上要求 P、Q两点，使得 PA+PQ+QB的值最小。 ( 原理用平移知识解)（1）点 A、B 在直线 m两侧：mnAPmnABmnAPmnAA'BmOAP'PmOBAB'mOAPmOABA'mABQPmABCQP4lBA过 A 点作 AC∥m,且 AC长等于 PQ长，连接 BC,交直线 m于 Q,Q向左移动 PQ长，即为 P 点，此时 P、Q即为所求的点。（2）点 A、 B在直线 m同侧：四、求两线段差的最大值问题(运用三角形两边之差小于第三边)1、在一条直线m上，求一点P，使 PA与 PB的差最大；（1）点 A、 B在直线 m同侧：（2）点 A、 B在直线 m异侧：过 B 作关于直线m的对称点 B’, 连接 AB’交点直线m于 P, 此时 PB=PB’， PA-PB最大值为AB’Ⅰ．专题精讲最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求“变动的两线段之和的最小值”时，大都应...