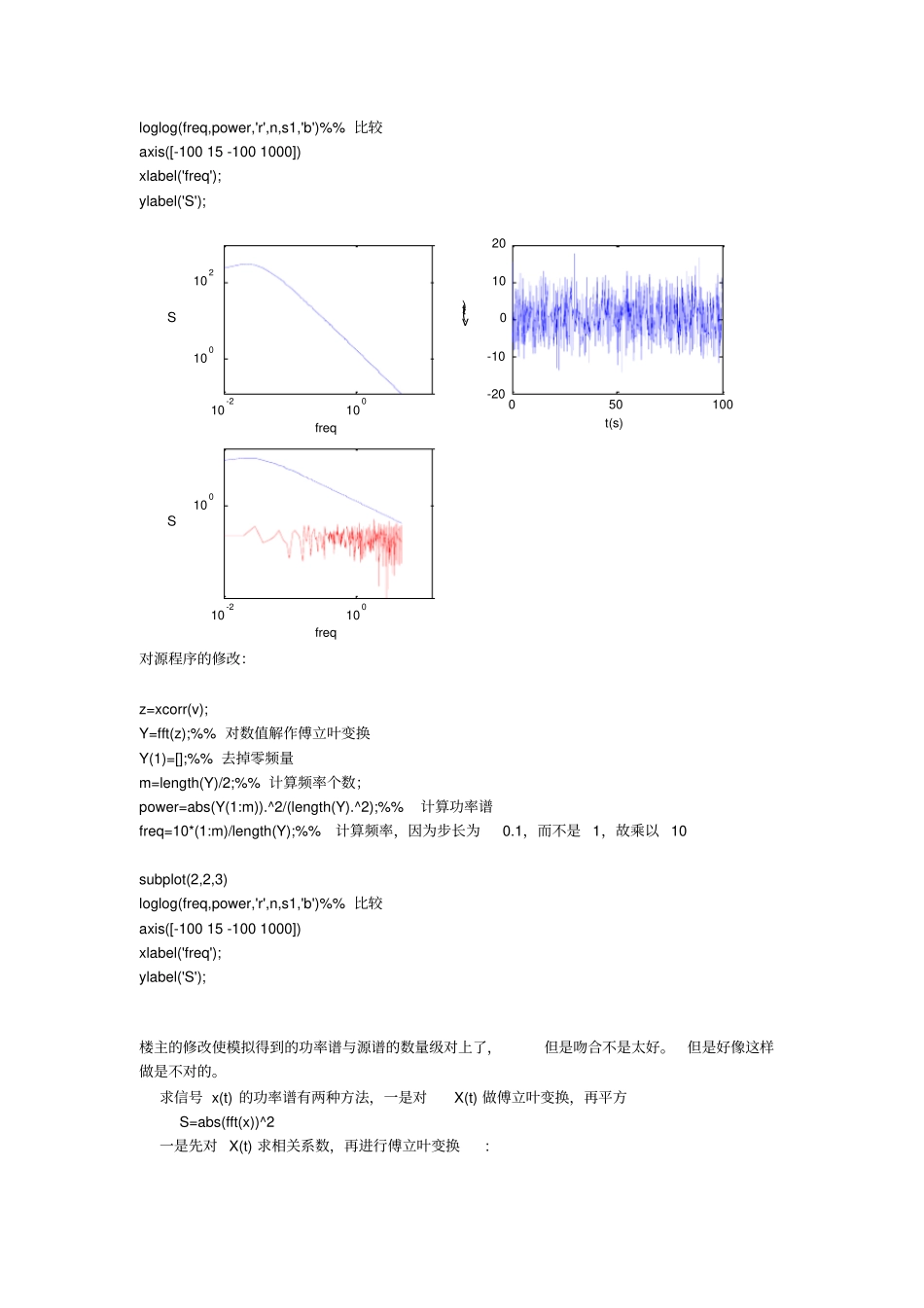
根据风的记录, 脉动风可作为高斯平稳过程来考虑。观察 n 个具有零均值的平稳高斯过程,其谱密度函数矩阵为:)(...)()(............)(...)()()(...)()()(212222111211nnnnnnsssssssssS(9)将)(S进行 Cholesky 分解,得有效方法。THHS)()()(*(10)其中,)(...)()(............0...)()(0...0)()(21222111nnnnHHHHHHH(11)TH)(*为)(H的共轭转置。根据文献 [8] ,对于功率谱密度函数矩阵为)(S的多维随机过程向量,模拟风速具有如下形式:jmNlmlljmlljmjtHtv11)(cos2)()(nj...,3,2,1(12)其中,风谱在频率范围内划分成N 个相同部分,N 为频率增量,)(ljmH为上述下三角矩阵的模,)(ljm为两个不同作用点之间的相位角,ml 为介于 0 和 2之间均匀分布的随机数,ll是频域的递增变量。文中模拟开孔处的来流风,因而只作单点模拟。即式(4)可简化为:NlllltHtv1cos2)()((13)本文采用 Davenport 水平脉动风速谱:3/422210)1(4)(xnkxvnSv(14)式中,--)(nSv脉动风速功率谱;--n脉动风频率 (Hz) ;--k地面粗糙度系数;;120010vnx--10v标准高度为10m 处的风速 (m/s)。Matlab 程序 : N=10; d=0.001; n=d:d:N;%% 频率区间( 0.01~10)v10=16; k=0.005; x=1200*n/v10; s1=4*k*v10^2*x.^2./n./(1+x.^2).^(4/3);%%Davenport谱subplot(2,2,1) loglog(n,s1)%% 画谱图axis([-100 15 -100 1000]) xlabel('freq'); ylabel('S'); for i=1:1:N/d H(i)=chol(s1(i));%%Cholesky分解end thta=2*pi*rand(N/d,1000);%%介于 0 和 2pi 之间均匀分布的随机数t=1:1:1000;%% 时间区间( 0.1~100s)for j=1:1:1000 a=abs(H); b=cos((n*j/10)+thta(:,j)'); c=sum(a.*b); v(j)=(2*d).^(1/2)*c;%%风荷载模拟end subplot(2,2,2) plot(t/10,v)%% 显示风荷载xlabel('t(s)'); ylabel('v(t)'); Y=fft(v);%% 对数值解作傅立叶变换Y(1)=[];%% 去掉零频量m=length(Y)/2;%% 计算频率个数;power=abs(Y(1:m)).^2/(length(Y).^2);%%计算功率谱freq=10*(1:m)/length(Y);%%计算频率,因为步长为0.1,而不是 1,故乘以 10 subplot(2,2,3) loglog(freq,power,'r',n,s1,'b')%% 比较axis([-100 15 -100 1000]) xlabel('freq'); ylabel('S'); 10-2100100102freqS050100-20-1001020t(s)v(t)10-2100100freqS对源程序的修改:z=xcorr(v); Y=fft(z);%% 对数值解作傅立叶变换Y(1)=[];%% 去掉零频量m=length(Y)/2;%% 计算频率个数;power=abs(Y(1:m)).^2/(length(Y).^2);%%计算功率谱freq=10*(1:m)/length(Y);%%计算频率,因为步长为0.1,而不是 1,故乘以 10 subplot(2,2,3) loglog(freq,power,'r',n,s1,'b')%% 比较axis([-100 15 -100 1000]) xlabel('freq'); ylabel('S'); 楼主的修改使模拟得到的功率谱与源谱的数量级对上了,但是吻合不是太好。但是好像这样做是不对的。求信号 x(t) 的功率谱有两种方法,一是对X(t) 做傅立叶变换,再平方 S=abs(fft(x))^2 一是先对 X(t) 求相关系数,再进行傅立叶变换: S=fft(xcorr(X)) 楼主的方法好像是这两个方法的混合。欢迎大家拍砖^_^