材料力学应力圆法课件VIP免费

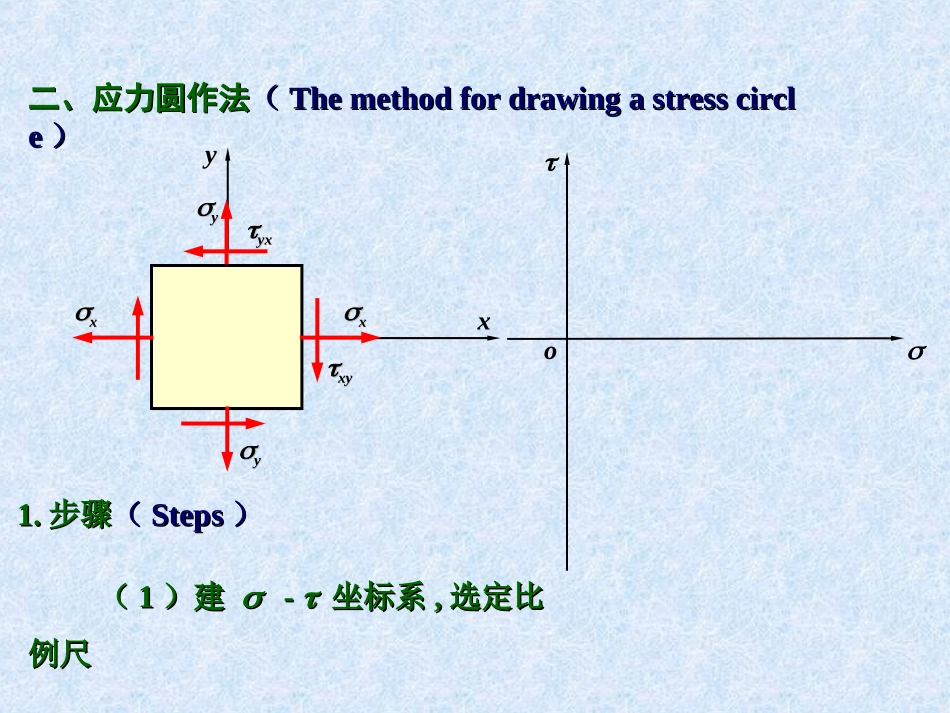
§§7-37-3平面应力状态分析平面应力状态分析--图解法图解法(Analysisofplanestress-statewith(Analysisofplanestress-statewithgraphicalmeans)graphicalmeans)cossinsincos2222222xyyxxyyxyx一、莫尔圆一、莫尔圆（（Mohr’scircleMohr’scircle））将斜截面应力计算公式改写为将斜截面应力计算公式改写为把上面两式等号两边平方把上面两式等号两边平方,,然后相加便可消去然后相加便可消去,,得得222222xyyxyx)()(因为因为xx,,yy,,xyxy皆为已知量皆为已知量,,所以上式是一个以所以上式是一个以,,为为变量的圆周方程变量的圆周方程..当斜截面随方位角当斜截面随方位角变化时变化时,,其上的应力其上的应力,,在在--直角坐标系内的轨迹是一个圆直角坐标系内的轨迹是一个圆..1.1.圆心的坐标圆心的坐标（（CoordinateofcircleceCoordinateofcirclecenternter））),(02yxC2.2.圆的半径圆的半径（（RadiusofcirclRadiusofcirclee））222xyyxR)(此圆习惯上称为此圆习惯上称为应力圆应力圆（（planestresscircleplanestresscircle））,,或称为或称为莫尔圆莫尔圆（（Mohr’scircleMohr’scircle））（（11）建）建--坐标系坐标系,,选定比选定比例尺例尺o二、应力圆作法二、应力圆作法（（ThemethodfordrawingastresscirclThemethodfordrawingastresscirclee））1.1.步骤步骤（（StepsSteps））xyxxxxyxyxxyxyyyyyDxyo（（22）量）量取取OA=OA=xxADAD==xyxy得得DD点点xyxxxxyxyxxyxyxAOB=OB=yy（（33）量）量取取BD′=BD′=yxyx得得D′D′点点yBByxD′（（44）连接）连接DD′DD′两点的直线与两点的直线与轴相交于轴相交于CC点点（（55）以）以CC为圆心为圆心,,CDCD为半径作圆为半径作圆,,该圆就是相应于该单该圆就是相应于该单元体的应力圆元体的应力圆CC（（11）该圆的圆心）该圆的圆心CC点点到坐标原点的距离为到坐标原点的距离为（（22）该圆半径为）该圆半径为222xyyxR)(DxyoxAyBByxD′CC2.2.证明证明(Prove)(Prove)22121yxOBOAOBOAOBOC)()(22222xyyxADCACD)(2yx三、应力圆的应用三、应力圆的应用（（Applicationofstress-circleApplicationofstress-circle））1.1.求单元体上任一截面上的应力求单元体上任一截面上的应力（（DeterminethestressesoDeterminethestressesonanyinclinedplanebyusingstress-circlenanyinclinedplanebyusingstress-circle））从应力圆的半径从应力圆的半径CDCD按方位角按方位角的转向转动的转向转动22得到半得到半径径CE.CE.圆周上圆周上EE点的坐标就依次为斜截面上的正应力点的坐标就依次为斜截面上的正应力和切应和切应力力..DxyoxAyBByxD′CC2200FEE22xyaxxxxyxyxxyxyeeffnn)22cos(0CEOCCFOCOF222200sinsincoscosCDCDOC2222sincosxyyxyx22222200sincoscossin)sin(CDCDCEFEo222cossinxyyx证明：证明：（（11）点面之间的对应关系）点面之间的对应关系::单元体某一面上的应力单元体某一面上的应力,,必对应于应力圆上某一点的坐标必对应于应力圆上某一点的坐标..说明说明AB（（22）夹角关系）夹角关系::圆周上任意两点所引半径的夹角等于圆周上任意两点所引半径的夹角等于单元体上对应两截面夹角的两倍单元体上对应两截面夹角的两倍..两者的转向一致两者的转向一致..22OOCCBBA2.2.求主应力数值和主平面位置求主应力数值和主平面位置（（DetermineprinciplestresDetermineprinciplestressandthedirectionofprinciplesandthedirectionofprincipleplanebyusingstresscircleplanebyusingstresscircle））（（11）主应力数值）主应力数值AA11和...