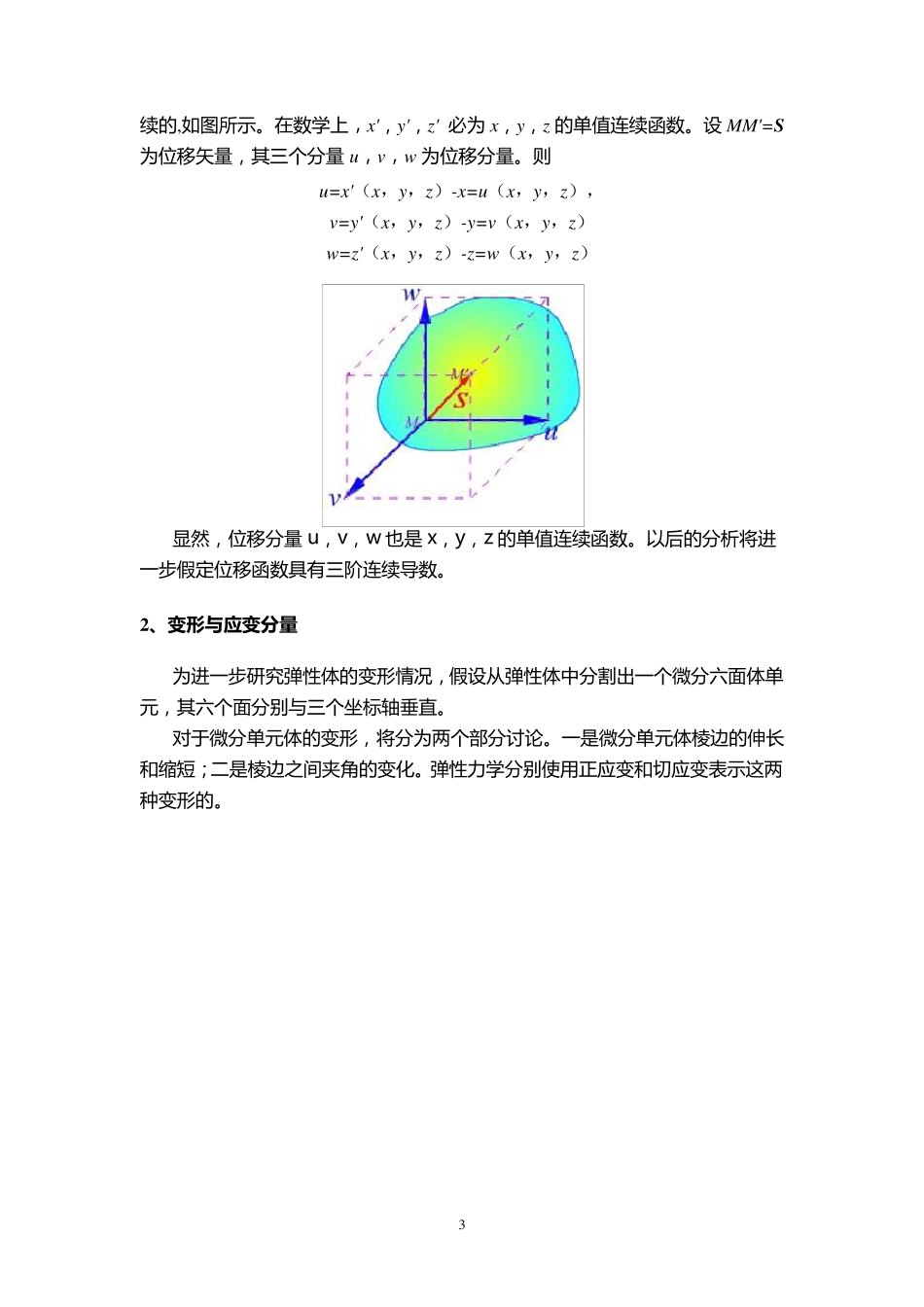
1 第 三 章 应 变 状 态 分 析 知 识 点 位 移 与 变 形 正 应 变 纯 变 形 位 移 与 刚 性 转 动位 移 应 变 分 量 坐 标 转 轴 公 式 主 应 变 齐 次 方 程 组 体 积 应 变 变 形 协 调 方 程 变 形 协 调 方 程 证 明 变 形 与 应 变 分 量 切 应 变 几 何 方 程 与 应 变 张 量 位 移 增 量 的 分 解 应 变 张 量 应 变 状 态 特 征 方 程 变 形 协 调 的 物 理 意 义 变 形 协 调 方 程 的 数 学 意 义 多 连 域 的 变 形 协 调 一 、内容介绍 本 章 讨 论 弹 性 体 的 变 形 , 物 体 的 变 形 是 通 过 应 变 分 量 确 定 的 。 因 此 , 首 先 确定 位 移 与 应 变 分 量 的 基 本 关 系 - 几 何 方 程 。 由 于 应 变 分 量 和 刚 体 转 动 都 是 通 过 位移 导 数 表 达 的 , 因 此 必 须 确 定 刚 体 转 动 位 移 与 纯 变 形 位 移 的 关 系 , 才 能 完 全 确 定一 点 的 变 形 。 对 于 一 点 的 应 变 分 量 , 在 不 同 坐 标 系 中 是 不 同 的 。 因 此 , 应 变 状 态 分 析 主 要是 讨 论 不 同 坐 标 轴 的 应 变 分 量 变 化 关 系 。 这 个 关 系 就 是 应 变 分 量 的 转 轴 公 式 ; 根据 转 轴 公 式 , 可 以 确 定 一 点 的 主 应 变 和 应 变 主 轴 等 。 当 然 , 由 于 应 变 分 量 满 足 二阶 张 量 变 化 规 律 , 因 此 具 体 求 解 可 以 参 考 应 力 状 态 分 析 。 应 该 注 意 的 问 题 是 变 形 协 调 条 件 , 就 是 位 移 的 单 值 连 续 性 质 。 假 如 位 移 函 数不 是 基 本 未 知 量 , 由 于 弹 性 力 学 是 从 微 分 单 元 体 入 手 讨 论 的 , 因 此 变 形 后 的 微 分单 元 体 也 必 须 满 足 连 续 性 条 件 。 这 在 数 学 上 , 就 是 应 变 分 量 必 须 满 足 变 形 协 调 方程 。 在 弹 性 体 的 位 移 边 界 , 则 必 须 满 足 位 移 边 界 条 件 。 二、重...