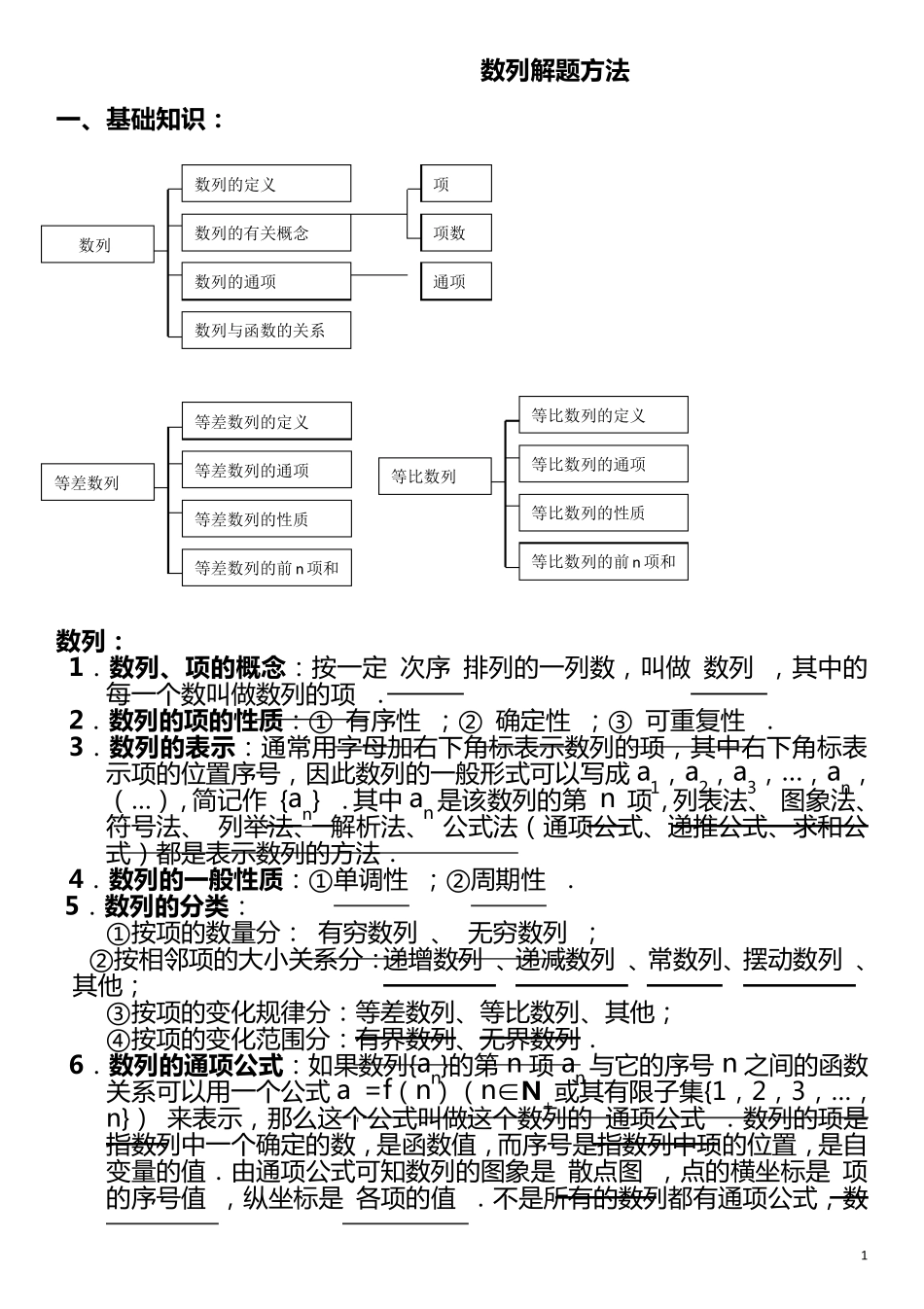
1 数 列 解 题 方 法 一 、基础知识: 数 列 : 1. 数 列 、项的概念: 按 一 定 次 序 排 列 的 一 列 数 , 叫 做 数 列 , 其 中 的每 一 个 数 叫 做 数 列 的 项 . 2. 数 列 的项的性质: ① 有 序 性 ; ② 确 定 性 ; ③ 可 重 复 性 . 3. 数 列 的表示: 通 常 用 字 母 加 右 下 角 标 表 示 数 列 的 项 , 其 中 右 下 角 标 表示 项 的 位 置 序 号 , 因 此 数 列 的 一 般 形 式 可 以 写 成 a1, a2, a3, …, an,( …) , 简 记 作 {an} . 其 中 an是 该 数 列 的 第 n 项 , 列 表 法 、 图 象 法 、 符 号 法 、 列 举 法 、 解 析 法 、 公 式 法 ( 通 项 公 式 、 递 推 公 式 、 求 和 公式 ) 都 是 表 示 数 列 的 方 法 . 4. 数 列 的一 般性质: ① 单 调 性 ; ② 周 期 性 . 5. 数 列 的分类: ① 按 项 的 数 量 分 : 有 穷 数 列 、 无 穷 数 列 ; ② 按 相 邻 项 的 大 小 关 系 分 : 递 增 数 列 、 递 减 数 列 、 常 数 列 、 摆 动 数 列 、其 他 ; ③ 按 项 的 变 化 规 律 分 : 等 差 数 列 、 等 比 数 列 、 其 他 ; ④ 按 项 的 变 化 范 围 分 : 有 界 数 列 、 无 界 数 列 . 6. 数 列 的通项公式: 如 果 数 列 {an}的 第 n 项 an与 它 的 序 号 n 之 间 的 函 数关 系 可 以 用 一 个 公 式 an=f( n) ( n∈N+或其 有 限子集{1, 2, 3, …,n}) 来表 示 , 那么这个 公 式 叫 做 这个 数 列 的 通 项 公 式 . 数 列 的 项 是指数 列 中 一 个 确 定 的 数 , 是 函 数 值, 而序 号 是 指数 列 中 项 的 位 置 , 是 自变 量 的 值. 由通 项 公 式 可 知数 列 的 图 象 是 散点图 , 点的 横坐标 是 项的 序 号 值 , 纵坐标 是 各项 的 值 . 不是 所有 的 数 列 都 有 通 项 公 式 , 数数列 数列的定义 数列的有关概念 数列的通项 数列与函数的关系 项 项数 通项 等差数列 等差数列的定义 等...