数列知识点归纳及习题总结

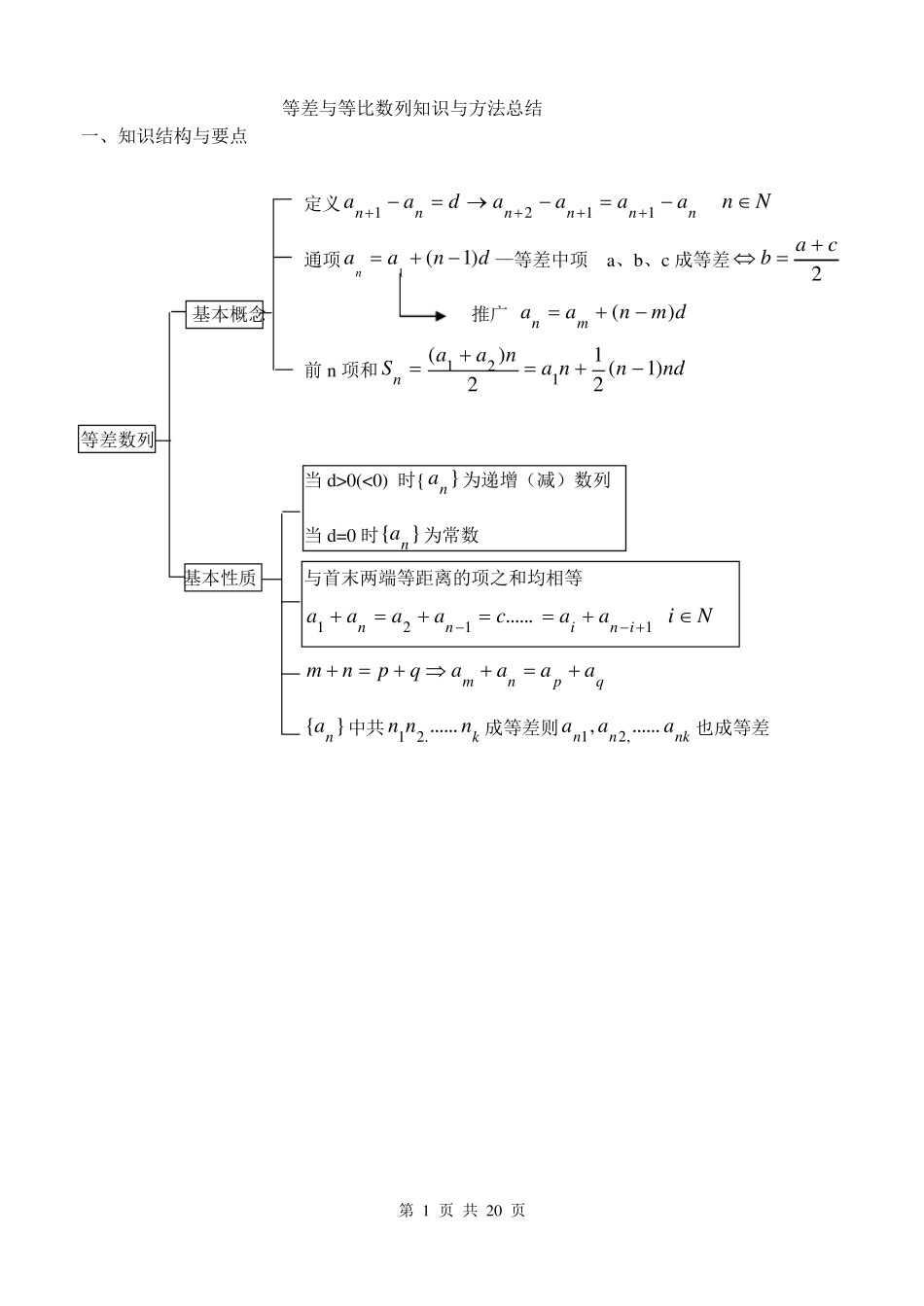
第 1 页 共 20 页 等差与等比数列知识与方法总结 一、知识结构与要点 定义nnnnnnaaaadaa1121 Nn 通项dnaan)1(1—等差中项 a、b、c 成等差2cab 基本概念 推广 dmnaamn)(  前 n 项和ndnnanaaSn)1(212)(121 等差数列 当 d>0(<0) 时{}na为递增（减）数列 当 d=0 时}{ na为常数 基本性质 与首末两端等距离的项之和均相等 1121......ininnaacaaaa Ni  qpnmaaaaqpnm }{ na中共knnn.......21成等差则nknnaaa......,,21也成等差 第 2 页 共 20 页 定义:nnnnnnaaaaqaa1121 Nn 通项 11nnqaa等比中项：a b c 成等比数列acb2 基本概念 推广mnmnqaa 前n 项和nS )1(11)1()1(111qqqaaqqaqnann 等比数列 与首末两端等距离的两项之积相等 1121......ininnaaaaaa qpnmaaaaqpnm }{ na成等比，若knnn,...,21 成等差则nknaaa,...,21 成等比 基本性质 当101qa 或 1001qa 时 {}na为递增数列 当 101qa或 1001qa 时 {}na为递减数列 当 q<0 时 {}na为摆动数列 当 q=1 时 {}na为常数数列 二、等差数列、等比数列基础知识与方法概括 （一）．一般数列 数列的定义及表示方法；数列的项与项数；有穷数列与无穷数列；递增（减）、摆动、循环数列；数列{an}的通项公式 an；数列的前n 项和公式 Sn； 一般数列的通项an 与前n 项和Sn 的关系：)2()1(111nSSnSaannn 第 3 页 共 20 页 （二）等差数列 1．等差数列的概念 [定义]如果一个数列从第2 项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示。 即：成等比数列}{)0,0,2(1nnnnaqandaa 2．等差数列的判定方法 （1）定义法：对于数列 na，若daann1(常数)，则数列 na是等差数列。 （2）等差中项法：对于数列 na，若212nnnaaa，则数列 na是等差数列。 3．等差数列的通项公式 如果等差数列 na的首项是1a ，公差是d ，则等差数列的通项为dnaan)1(1。 [说明]：该公式整理后是关于n 的一次函数。 4．等差数列的前n 项和 （1）．2)( 1nnaanS （ 2.） dnnnaS...